A figura mostra uma barra de comprimento que é forçada a se mover com velocidade constante ao longo de trilhos horizontais.

Os trilhos são conectados à direita por um fio condutor. A barra, os trilhos e o fio formam assim uma espira condutora. A resistência elétrica da barra vale , a resistência do resto da espira é desprezível. Uma corrente que percorre um fio longo situado a uma distância a da espira produz um campo magnético (não uniforme) que atravessa a espira (como mostrado em figura).

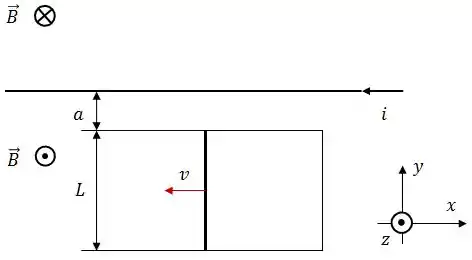
Nestas condições, determine:

a força eletromotriz induzida na espira;

a corrente induzida na espira;

a potência dissipada da espira;

o módulo, a direção e o sentido da força que deve ser aplicada à barra por um agente externo para que esta se mova com velocidade constante.

(Esta questão compõe-se de 3 itens independentes.)

Uma bateria de constante é conectada a um indutor num circuito de malha simples. A resistência equivalente do circuito vale . No instante em que a bateria é ligada no indutor, a corrente é nula. Sabendo que a corrente que atravessa o circuito é dada pela função , calcule o valor da indutância .

Um capacitor inicialmente carregado com , é conectado a um indutor pelo qual inicialmente não passa corrente. A resistência equivalente deste circuito de malha simples vale . Encontre a expressão da carga no capacitor em função do tempo, .

O circuito oscilante da figura possui resistência desprezível. O capacitor vale e, em , possui carga . O indutor, também em , possui energia e está sendo atravessado pela corrente com o sentido mostrado na figura. Calcule a carga máxima no capacitor.

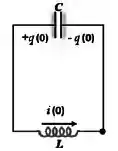
(SUGESTÃO: Lembre-se da conservação de energia). Use

O fluxo magnético através de uma espira circular de diâmetro e resistência , obedece à seguinte equação:

Sabendo que:

• Em , ;
• Em , e ;

Encontre os valores de e com as unidades corretas e escreva a expressão final para o fluxo magnético (considere e ).

Suponha agora uma nova situação em que o campo magnético através da mesma espira obedeça à seguinte equação: , onde e são constantes a determinar.

Sabendo que nesta nova situação em , e em , encontre os valores das constantes e com as respectivas unidades e escreva a expressão final para o campo magnético e para induzida.

Passo 1

Encontre os valores de e com as unidades corretas e escreva a expressão final para o fluxo magnético (considere e ).

Vamos utilizar as 3 condições que o problema nos deu para encontrar os valores de e , ok?

• Em , ;
• Em , ;
• Em , ;

Por definição, como a área da espira é constante, podemos dizer que , logo:

Derivando o campo magnético em função do tempo, teremos:

Onde:

Portanto:

Passo 2

Beleza, nós já conseguimos determinar quem é , agora vamos ter que resolver o sistema abaixo pra determinar quem é e .

Multiplicando a primeira linha por 3, teremos:

Fazendo a primeira equação menos a segunda, teremos:

Agora, multiplicando a primeira linha por 2 e, depois, fazendo a segunda equação menos a primeira, encontraremos:

Até aqui, beleza, mas quais são as unidades de e ?

Passo 3

Vamos voltar à equação original que o problema nos deu.

Se os três termos estão se somando, eles necessariamente tem as mesmas unidades de medida que, nesse caso, são de fluxo magnético , então basta fazermos uma análise dimensional.

Para , teremos:

Para , teremos:

Finalmente:

Pra finalizar:

Agora sim, acabamos a letra !

Passo 4

Sabendo que nesta nova situação em , e em , encontre os valores das constantes e com as respectivas unidades e escreva a expressão final para o campo magnético e para induzida.

Pra começar, vamos logo determinar as unidades de medida desses caras?

Como a função exponencial é adimensional, deve ter a mesma unidade de , logo:

E como o expoente também deve ser algo adimensional:

Bom, beleza... já podemos nos preocupar só em calcular os valores de e .

A estratégia aqui é a mesma que usamos na letra , vamos usar as condições que o problema nos deu para determinar os valores desses caras:

• em ;
• em ;

Finalmente: