Força e Torque sobre uma Espira, Lei de Ampère, Lei de Faraday, Lei de Lenz
A figura mostra uma barra de comprimento que é forçada a se mover com velocidade constante ao longo de trilhos horizontais.
Os trilhos são conectados à direita por um fio condutor. A barra, os trilhos e o fio formam assim uma espira condutora. A resistência elétrica da barra vale , a resistência do resto da espira é desprezível. Uma corrente que percorre um fio longo situado a uma distância a da espira produz um campo magnético (não uniforme) que atravessa a espira (como mostrado em figura).
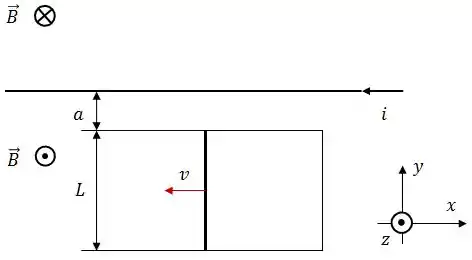
Nestas condições, determine:
a força eletromotriz induzida na espira;
a corrente induzida na espira;
a potência dissipada da espira;
o módulo, a direção e o sentido da força que deve ser aplicada à barra por um agente externo para que esta se mova com velocidade constante.
Passo 1
a força eletromotriz induzida na espira;
A induzida é determinada através da Lei de Faraday, dada por:
O fluxo magnético é dado por:
Então precisamos começar calculando o campo magnético gerado pelo fio.
Esse campo pode ser calculado através da Lei de Ampère, dada por:
Onde é a corrente que passa por dentro da amperiana que, nesse caso, vale . Como se trata de um fio, o campo magnético a uma distância do fio é dada por:
Passo 2
O fluxo magnético é dado por:
Onde é um pedaço infinitesimal da área.
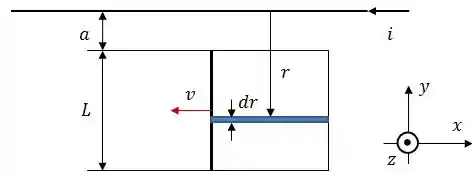
Logo:
Assim, substituindo isso na expressão do fluxo magnético, teremos:
Passo 3
Finalmente, a induzida é dada por:
Logo:
Como queremos somente a , não precisamos nos preocupar com o sinal.
Passo 4
a corrente induzida na espira;
Agora que já temos a induzida, para calcular a corrente induzida, basta usar a Lei de Ohm:
Substituindo a expressão de , teremos:
Passo 5
a potência dissipada da espira;
Por definição, a potência dissipada é dada por:
Logo, substituindo a expressão de , teremos:
Passo 6
o módulo, a direção e o sentido da força que deve ser aplicada à barra por um agente externo para que esta se mova com velocidade constante.
A força aplicada à barra para que permaneça com velocidade constante deve ter o módulo, a mesma direção e sentido oposto ao da força magnética sobre a barra, gerada pelo campo magnético .
A força magnética sobre a barra, por definição, é dada por:
Nessa fórmula, é um vetor na mesma direção e sentido da corrente induzida. Isso significa que precisamos descobrir o sentido da corrente induzida.
Para isso, vamos recorrer à Lei de Lenz, que diz:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
Resumindo, o que ela quer dizer é o seguinte:
Se o fluxo magnético estiver aumentando na espira, o campo magnético induzido vai estar no sentido contrário ao campo magnético externo.
Se o fluxo magnético estiver diminuindo na espira, o campo magnético induzido vai estar no mesmo sentido do campo magnético externo.
Nesse caso, o fluxo magnético é dado por:
Como está aumentando com o tempo, o fluxo magnético também está aumentando, isso significa que o campo magnético vai estar no sentido contrário ao campo magnético externo, ou seja, entrando na página.
Para que isso ocorra, a corrente induzida tem que estar no sentido horário.
Voltando ao problema...
Passo 7
Graficamente, vamos dar uma olhada no que está acontecendo:
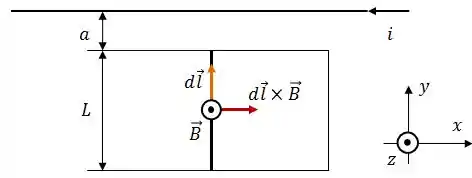
Daqui, podemos tirar que:
Logo:
Integrando esse cara de até , teremos:
Assim, como a barra se movimenta com velocidade constante:
FINALMENTE:
Resposta