P3 de Física 3 - FIS1051 da PUCRIO - 2017.2

Um solenoide com comprimento muito maior do que o seu raio (solenoide ideal) tem o eixo de simetria coincidente com o eixo , e é atravessado por uma corrente (conhecida) em direção anti-horária (veja a figura).

A densidade linear de voltas do solenoide varia com a coordenada e é dada pela equação . Uma espira condutora circular de resistência elétrica e raio (conhecidos) é introduzida no solenoide e é colocada no instante de tempo no início do solenoide , para depois ser movida por um sistema não mostrado com velocidade constante positiva ao longo do eixo . A espira é completamente contida no solenoide (como mostrado na figura).

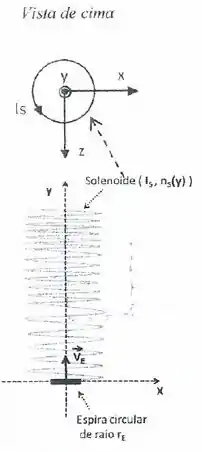
Nestas condições:

(a) Calcule em função do tempo o campo magnético (módulo, direção e sentido) gerado pelo solenoide no centro da espira.

(b) Calcule a corrente induzida na espira.

(c) Calcule o campo magnético (módulo, direção e sentido) gerado somente pela corrente induzida no centro da espira (Sugestão: utilize Biot e Savart). Qual será o campo magnético total no centro da espira?

No circuito em corrente alternada da figura, o capacitor é variável, com uma capacitância que pode ser regulada de zero até . O circuito é alimentado por uma fonte de tensão senoidal com valor máximo e frequência . Além disso, o resistor e o indutor possuem os seguintes valores: e .

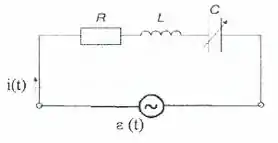
Nestas condições (nas contas, considere ):

(a) Calcule o valor da capacitância para que o fator de potência do circuito seja igual a . O circuito tem comportamento capacitivo ou indutivo? Justifique suas afirmações

(b) Calcule o valor máximo da corrente e as tensões no resistor , no capacitor e no indutor . Desenhe também o diagrama dos fasores (em escala).

(c) Qual valor deve ter para que o circuito entre em ressonância? Calcule nesta nova condição o valor médio da potência dissipada no resistor.

Considere um plano isolante infinito situado em com uma densidade superficial de carga , como indicado na Figura 1. Tomando como o ponto de referência para o potencial, encontre o potencial nas seguintes regiões:

(a) .

(b) .

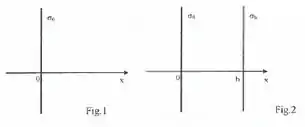
Suponha que no ponto seja colocado um plano isolante infinito com uma densidade superficial de carga (Figura 2).

(c) Nesta nova situação, encontre o potencial na região entre as duas placas.

(d) Considere agora que uma partícula de massa e carga é colocada em repouso em . Em que direção a partícula se move? Encontre a velocidade final dela ao atingir a placa.