Considere um plano isolante infinito situado em com uma densidade superficial de carga , como indicado na Figura 1. Tomando como o ponto de referência para o potencial, encontre o potencial nas seguintes regiões:
(a) .
(b) .
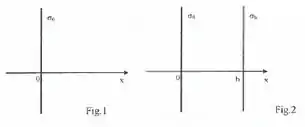
Suponha que no ponto seja colocado um plano isolante infinito com uma densidade superficial de carga (Figura 2).
(c) Nesta nova situação, encontre o potencial na região entre as duas placas.
(d) Considere agora que uma partícula de massa e carga é colocada em repouso em . Em que direção a partícula se move? Encontre a velocidade final dela ao atingir a placa.
Passo 1
Para resolver o primeiro caso (Figura 1), vamos lembrar inicialmente qual é o campo elétrico gerado por um plano infinito de densidade superficial de cargas :
Ah, caso você queira provar matematicamente esse valor aí de cima, a dica é usar Lei de Gauss com uma superfície gaussiana cilíndrica, com eixo perpendicular ao plano carregado. Beleza?
Passo 2
Bem, sabemos o valor de , agora podemos calcular o potencial da seguinte forma:
onde é o vetor de deslocamento, apontando na direção do plano, e está orientado para fora do plano. Isso significa que . Vamos assumir que
Temos que:
A resposta acima é válida tanto para , quanto para .
Passo 3
No segundo caso (Figura 2), o módulo campo elétrico entre as placas carregadas é dado por:
apontando da placa positiva para a negativa. Novamente, poderíamos obter o valor de utilizando Lei de Gauss utilizando uma superfície gaussiana cilíndrica.
Passo 4
Vamos calcular o potencial para um ponto entre as placas. Temos:
onde é o vetor de deslocamento, apontando agora na direção do eixo , sentido negativo, e também aponta na direção do eixo , mas no sentido positivo. Isso significa que . Vamos assumir que
Temos:
Passo 5
Por fim, vamos resolver o item (d). Como a partícula possui carga positiva, ela se desloca no sentido da placa negativa, ou seja, até o ponto .
A energia cinética final, ou seja, quando a partícula atinge , é dada por:
A energia cinética inicial, ou seja, em é nula, pois a partícula está inicialmente em repouso.
Vamos considerar que a energia potencial elétrica em é nula. Já para , temos que:
Portanto, por conservação de energia:
Resposta
(a)
(b)
(c)
(d)