Um solenoide com comprimento muito maior do que o seu raio (solenoide ideal) tem o eixo de simetria coincidente com o eixo , e é atravessado por uma corrente (conhecida) em direção anti-horária (veja a figura).
A densidade linear de voltas do solenoide varia com a coordenada e é dada pela equação . Uma espira condutora circular de resistência elétrica e raio (conhecidos) é introduzida no solenoide e é colocada no instante de tempo no início do solenoide , para depois ser movida por um sistema não mostrado com velocidade constante positiva ao longo do eixo . A espira é completamente contida no solenoide (como mostrado na figura).
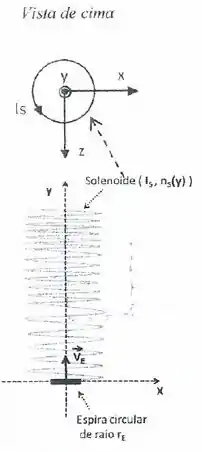
Nestas condições:
(a) Calcule em função do tempo o campo magnético (módulo, direção e sentido) gerado pelo solenoide no centro da espira.
(b) Calcule a corrente induzida na espira.
(c) Calcule o campo magnético (módulo, direção e sentido) gerado somente pela corrente induzida no centro da espira (Sugestão: utilize Biot e Savart). Qual será o campo magnético total no centro da espira?
Passo 1
Vamos utilizar a Lei de Ampère para determinar o campo magnético no interior do solenoide. Temos que:
Vamos escolher um retângulo como percurso fechado, com lado coincidente com o eixo do solenoide iniciando na origem até um comprimento e o lado paralelo ao eixo, mas do lado de fora do solenoide. Assim sendo, temos:
- Ao longo dos lados e , é perpendicular à ;
- Ao longo do lado , ; e
- Ao longo do lado , temos:
Passo 2
Vamos analisar agora o lado direito da equação da Lei de Ampère. Precisamos calcular o número de espiras contidas no comprimento para determinar a corrente interna .
A partir da densidade linear de voltas, temos que:
Portanto, a corrente total no interior do retângulo é dada por: . Assim sendo,
Passo 3
Temos o campo magnético em função de , agora precisamos descobrir o campo dentro da espira em função do tempo . Bem, sabemos que a espira está se movimentando com uma velocidade . Logo,
Ah, não podemos nos esquecer de determinar a direção e o sentido de . Pela regra da mão direita, aponta para cima, direção do eixo , sentido positivo.
Passo 4
Para calcular a corrente induzida na espira, calculamos inicialmente a fem induzida. Temos:
A corrente induzida, em módulo, é dada por:
De acordo com a Lei de Lenz, como o fluxo (para cima) está aumentando, a corrente induzida deve se opor a este aumento e, portanto, tem sentido horário.
Passo 5
Agora, vamos utilizar Biot-Savart para determinar o campo no centro da espira. Temos:
Substituindo o valor de , chegamos em:
Passo 6
Para terminar a questão, calculamos o campo magnético resultante no centro da espira:
Resposta
(a)
(b) , sentido horário.
(c) e