No circuito em corrente alternada da figura, o capacitor é variável, com uma capacitância que pode ser regulada de zero até . O circuito é alimentado por uma fonte de tensão senoidal com valor máximo e frequência . Além disso, o resistor e o indutor possuem os seguintes valores: e .
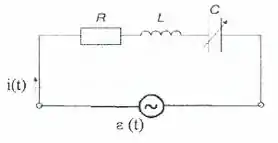
Nestas condições (nas contas, considere ):
(a) Calcule o valor da capacitância para que o fator de potência do circuito seja igual a . O circuito tem comportamento capacitivo ou indutivo? Justifique suas afirmações
(b) Calcule o valor máximo da corrente e as tensões no resistor , no capacitor e no indutor . Desenhe também o diagrama dos fasores (em escala).
(c) Qual valor deve ter para que o circuito entre em ressonância? Calcule nesta nova condição o valor médio da potência dissipada no resistor.
Passo 1
Bem, como o fator de potência é dado por:
Assim sendo,
com e . Temos:
O circuito é mais indutivo, pois .
Passo 2
Temos que:
Podemos calcular a partir da seguinte expressão:
As tensões no resistor, no capacitor e no indutor são dadas por:
Os fasores podem ser visualizados na figura abaixo.
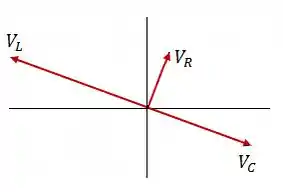
Passo 3
Qual valor deve ter para que o circuito entre em ressonância? Calcule nesta nova condição o valor médio da potência dissipada no resistor.
Para que o circuito entre em ressonância,
Nesse caso, e, portanto, . A corrente máxima é dada por:
A potência dissipada no resistor será:
Resposta
(a) .
(b) , e .
(c) e .