AV2 de Física 3 da UFJF - 2018.1

4 – Uma casca condutora cilíndrica muito longa de raio interno e raio externo transporta a corrente distribuída uniformemente por toda a área de sua seção transversal, entre e (ver a figura abaixo). Derive uma expressão para a magnitude do campo magnético devido a esta corrente, como uma função da distância radial do eixo central, para cada uma das seguintes regiões:

a)

1 – No circuito ao lado, uma bateria e quatro lâmpadas idênticas estão conectadas. Classifique a corrente em cada um dos pontos indicados (, , , , , , , e ), da corrente de maior módulo para a corrente de menor módulo. Use o sinal de “” (maior) ou de “” (igual). Nenhum elemento do circuito está aterrado.

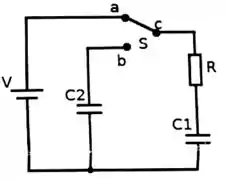
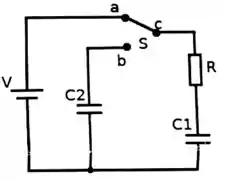
2 – No circuito da figura ao lado, uma fonte de está inicialmente ligada a uma chave , que pode ser configurada para ligaros pontos ou . Em cada ramo do circuito há um capacitor, ou , e um resistor em série com o capacitor . Os capacitores encontram-se descarregados inicialmente.

a) Quando a chave está na posição (a mesma da figura), temos a carga do capacitor . Supondo que a carga inicial deste capacitor seja nula, encontre a tensão no capacitor no instante inicial e após um longo tempo, quando o capacitor estiver totalmente carregado.

4 – Uma casca condutora cilíndrica muito longa de raio interno e raio externo transporta a corrente distribuída uniformemente por toda a área de sua seção transversal, entre e (ver a figura abaixo). Derive uma expressão para a magnitude do campo magnético devido a esta corrente, como uma função da distância radial do eixo central, para cada uma das seguintes regiões:

b)

2 – No circuito da figura ao lado, uma fonte de está inicialmente ligada a uma chave , que pode ser configurada para ligaros pontos ou . Em cada ramo do circuito há um capacitor, ou , e um resistor em série com o capacitor . Os capacitores encontram-se descarregados inicialmente.

b) Depois de um longo tempo, a corrente cessa no resistor . Neste instante, a chave é colocada na posição , e a contagem do tempo é zerada. Apresente a equação diferencial que rege as cargas dos capacitores e a corrente com o tempo.

c) Lembrando que a carga inicial do capacitor é nula, encontre uma expressão que descreve a corrente em função do tempo da nova configuração do circuito, com a chave na posição .

4 – Uma casca condutora cilíndrica muito longa de raio interno e raio externo transporta a corrente distribuída uniformemente por toda a área de sua seção transversal, entre e (ver a figura abaixo). Derive uma expressão para a magnitude do campo magnético devido a esta corrente, como uma função da distância radial do eixo central, para cada uma das seguintes regiões:

c)

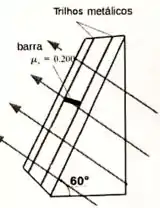
3 – Uma barra de metal de comprimento tem uma massa com suas extremidades apoiadas sobre trilhos metálicos. Os trilhos estão fixados sobre um plano inclinado que forma um ângulo com a horizontal. Os trilhos têm resistência elétrica desprezível, comparada à resistência da barra. Existe um campo magnético perpendicular à superfície inclinada em toda a região dos trilhos (ver figura abaixo). Os dois pontos de apoio nas extremidades da barra, em contato com os trilhos metálicos, permitem a passagem de corrente elétrica através da barra. Fecha-se o circuito com uma fonte de tensão ajustável conectada aos trilhos (fonte não representada na figura). O coeficiente de atrito estático entre a barra e os contatos é de . Quais as magnitudes e direções, mínima e máxima, da corrente que deve passar pela barra para impedir que ela se mova?

Dica: A força de atrito estático tem como módulo o valor máximo , onde é o modulo da força normal da superfície.