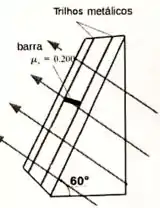
3 – Uma barra de metal de comprimento tem uma massa com suas extremidades apoiadas sobre trilhos metálicos. Os trilhos estão fixados sobre um plano inclinado que forma um ângulo com a horizontal. Os trilhos têm resistência elétrica desprezível, comparada à resistência da barra. Existe um campo magnético perpendicular à superfície inclinada em toda a região dos trilhos (ver figura abaixo). Os dois pontos de apoio nas extremidades da barra, em contato com os trilhos metálicos, permitem a passagem de corrente elétrica através da barra. Fecha-se o circuito com uma fonte de tensão ajustável conectada aos trilhos (fonte não representada na figura). O coeficiente de atrito estático entre a barra e os contatos é de . Quais as magnitudes e direções, mínima e máxima, da corrente que deve passar pela barra para impedir que ela se mova?
Dica: A força de atrito estático tem como módulo o valor máximo , onde é o modulo da força normal da superfície.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nessa questão temos uma barra condutora de comprimento e massa . Essa barra está em contado, em suas extremidades, com dois trilhos condutores de resistência nula sendo que nas extremidades dos trilhos, existe uma fonte de tensão, mas não sabemos em qual extremidade.
Esse sistema está em cima de uma rampa que faz um ângulo com a horizontal e está imerso em um campo magnético, , perpendicular ao sistema barra-trilhos assim como vemos na imagem do enunciado.
Existe atrito entre a barra e os trilhos cujo coeficiente de atrito estático é dado por .
Com essas informações, queremos saber qual o sentido e a magnitude da corrente e qual é o módulo da força magnética que faz a barra permanecer parada nos trilhos.
Tem ideia do que fazer nessa questão? 🤔🤔
Bora ver!
Passo 2
Esse problema engloba vários conhecimentos. Força de atrito, força gravitacional, força magnética...
Antes de tudo, vamos analisar a situação sem a corrente na barra.
Vamos desenhar o diagrama de forças que a barra sofre
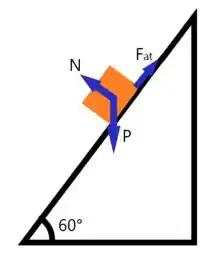
Sabemos que a força de atrito é dada por , já a normal é dada por .
Por sua vez, se , então
Foi dito no enunciado que , e . Como sabemos que , então
Com isso, vimos que aponta pra cima da rampa e tem magnitude .
Agora vamos analisar a força peso que empurra a barra para baixo.
No caso, o vetor que aponta para a base da tampa é dado por e vamos chamá-lo de .
Com isso, vemos que como , obrigatoriamente a corrente deve seguir um caminho que faça com que a força magnética aponte para cima.
Mas que direção é essa? 👀
Passo 3
A força magnética em um fio condutor segue a regra da mão direita, ou seja
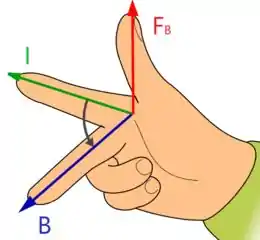
Como aponta para fora da rampa e deve apontar para cima, a corrente deve seguir da direita para a esquerda na barra.
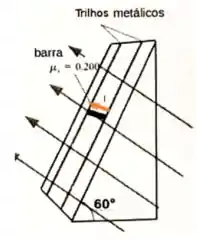
Pela lei de conservação de forças, a componente força peso deve ser igual a soma da força de atrito coma força magnética.
Mas tem outra possibilidade, não é? E se a força magnética for tão grande que se sobreponha a força peso. Dessa forma, a força de atrito apontará para baixo da rampa e para a barra permanecer parada, a soma entre a componente da força peso e a força de atrito deve ser igual a força magnética , ou seja
Só resta uma coisa, não é? Falda definir o que é a força magnética !
Bora lá! 😁
Passo 4
Como falamos no passo anterior, a força segue a regra da mão direita.
E sua fórmula para esse caso é dada por
Como é perpendicular ao nosso fio e como é constante, podemos reescrever essa fórmula como
Perceba que a integral de linha resulta no comprimento da barra, ou seja, . Com isso, temos
Substituindo e pelos valores dados no enunciado...
Estamos quase terminando! 😉
Passo 5
No primeiro caso, quando a barra está na iminência da queda, e anulam , ou seja
Como vimos que , e ...
Isolando
Nesse caso, a corrente tem modulo de ! 😎
E quando a barra está na iminência de subir? A força e a força anulam
Isolando
Já nesse caso, a corrente na barra deve ser igual a para que ela continue parada!
Portanto, para a barra permanecer parada, a corrente que passa por ela deve estar entre e , além de seguir o sentido da direita para a esquerda visto que a rampa está de frente para o observador.
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
