2 – No circuito da figura ao lado, uma fonte de está inicialmente ligada a uma chave , que pode ser configurada para ligaros pontos ou . Em cada ramo do circuito há um capacitor, ou , e um resistor em série com o capacitor . Os capacitores encontram-se descarregados inicialmente.
a) Quando a chave está na posição (a mesma da figura), temos a carga do capacitor . Supondo que a carga inicial deste capacitor seja nula, encontre a tensão no capacitor no instante inicial e após um longo tempo, quando o capacitor estiver totalmente carregado.
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

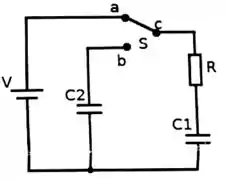
Nessa questão temos um circuito composto por uma fonte , dois capacitores ( e ). M resistor e uma chave como vemos na imagem do enunciado.
Inicialmente a chave está ligando e , dessa forma, após um longo período, o capacitor se carrega.
Se inicialmente o capacitor está descarregado, qual é a tensão no capacitor em e qual é a tensão quando o capacitor estiver totalmente carregado?
Tem ideia do que fazer? 🤔
Em um circuito a tensão em um capacitor que inicialmente está descarregado, é dada pela função
Essa função vem a partir da análise de malha do circuito resultando na função . E como , resultamos na função .
Vamos usá-la para responder nossas perguntas!
Bora lá! 😁
Passo 2
Como vimos que a tensão instantânea no capacitor que está inicialmente descarregado é dada por
No instante inicial, quando o capacitor está completamente descarregado, podemos admitir que .
Calculando , temos
Como qualquer número elevado a é igual a , vamos obter
Ou seja, a tensão no instante inicial que o capacitor começa a se carregar é igual a .
Interessante, não é? 🤩
Passo 3
Agora, vamos considerar que é muito maior que , de modo que tenda a
Assim, analisando apenas o termo , vamos obter .
O gráfico de se comporta como uma queda exponencial quanto aumenta, veja só
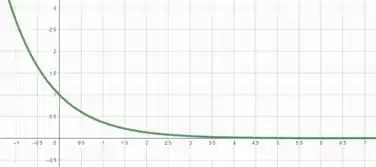
Logo, podemos dizer que .
Substituindo essa informação em , temos
Portanto, vemos que quando é muito grande e o capacitor está carregado, a sua tensão é igual a tensão da fonte! Isso faz sentido pois se o capacitor está carregado, não há mais a possibilidade de passagem de elétrons entre suas placas, ou seja, fica saturado!
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
