UFJF. Física 3. Prova AV2. 2018.1. Questão 4a.
4 – Uma casca condutora cilíndrica muito longa de raio interno e raio externo transporta a corrente distribuída uniformemente por toda a área de sua seção transversal, entre e (ver a figura abaixo). Derive uma expressão para a magnitude do campo magnético devido a esta corrente, como uma função da distância radial do eixo central, para cada uma das seguintes regiões:
a)
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse problema temos uma casca cilíndrica de raio interno e raio externo . Nessa casca, flui uma corrente uniforme homogeneamente em sua seção transversal.
Com isso, queremos obter a magnitude do campo magnético a uma distância do eixo central da casca, dado que .
E aí, como fazemos isso?? 🤔🤔
Para resolver esse problema, vamos apelar para a Lei de Ampère.
Essa lei nos diz que a integral de linha do campo magnético por uma curva fechada é igual a multiplicação entre a constante e a corrente envolvida por essa curva.
Sacou? Bora ver como é isso então! 😁
Passo 2
Na prática, essa lei é descrita pela equação
Vamos analisar a seção transversal para o nosso problema
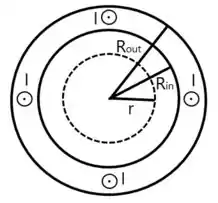
Dado que é menor que o raio interno , como vamos obter ?
Perceba que sem fazer conta nenhuma, vamos conseguir resolver esse problema.
Na definição da Lei de Ampère, falamos que a magnitude do campo magnético depende da constante e da corrente interna na região analisada.
Portanto, de é menor que , não há corrente interna na região, logo o campo magnético é nulo!
Tranquilo? 😎
É isso! Essa resolução te ajudou? Responde Aí! ✌