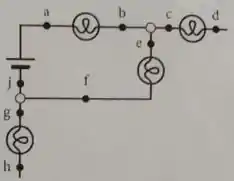
1 – No circuito ao lado, uma bateria e quatro lâmpadas idênticas estão conectadas. Classifique a corrente em cada um dos pontos indicados (, , , , , , , e ), da corrente de maior módulo para a corrente de menor módulo. Use o sinal de “” (maior) ou de “” (igual). Nenhum elemento do circuito está aterrado.

Substituindo nossas lâmpadas por resistências , temos

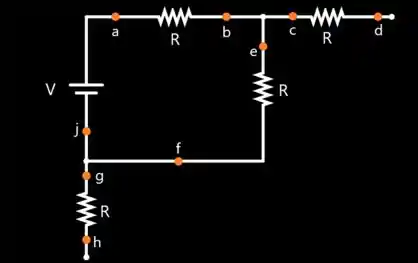
Vamos começar pelos resistores entre os pontos e e entre e . No enunciado do problema foi dito que não há aterramento no circuito, ou seja, essas lâmpadas não estão ligadas a nada para dar continuidade do circuito.

Na prática se tentássemos ligar um fio positivo em uma lâmpada sem que ligássemos o neutro, a lâmpada não iria funcionar pois o fui neutro ou o aterramento tem a função de gerar a diferença de potencial nesse caso e dar continuidade no circuito.

Com isso, podemos afirmar que esses dois resistores são “pesos de papel” pois não interferem no nosso circuito, logo, podemos desconsiderá-los! 😎

Com relação a corrente que flui entre os pontos , , e , podemos afirmar que é nula, ou seja

Tranquilo até aqui? 👍

Reescrevendo o circuito sem esses resistores, temos

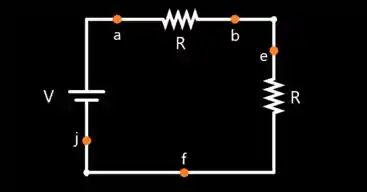
Vemos que o circuito resultante é um circuito de uma única malha!

Isso é fenomenal pois sabemos que a corrente se conserva em uma malha.

Pela lei de Ohm, vemos que (associando as duas resistências em série)

Se a corrente na malha é igual em todos os pontos, então

Colocando os pontos em ordem decrescente de corrente, temos

Portanto, os pontos dentro da malha fechada têm a mesma corrente e os pontos que estão fora da malha, com o circuito aberto, tem corrente menor.

É isso! Essa resolução te ajudou? Responde Aí! ✌