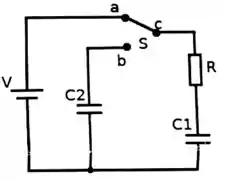
2 – No circuito da figura ao lado, uma fonte de está inicialmente ligada a uma chave , que pode ser configurada para ligaros pontos ou . Em cada ramo do circuito há um capacitor, ou , e um resistor em série com o capacitor . Os capacitores encontram-se descarregados inicialmente.
b) Depois de um longo tempo, a corrente cessa no resistor . Neste instante, a chave é colocada na posição , e a contagem do tempo é zerada. Apresente a equação diferencial que rege as cargas dos capacitores e a corrente com o tempo.
c) Lembrando que a carga inicial do capacitor é nula, encontre uma expressão que descreve a corrente em função do tempo da nova configuração do circuito, com a chave na posição .
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nesse problema, temos um circuito com uma fonte de tensão , dois capacitores ( e ), um resistor e uma chave .
Inicialmente a chave está ligando em e assim, o capacitor se carrega totalmente.
A partir desse instante, a chave passa a conectar os pontos e . Nosso objetivo é obter a equação que descreve as cargas e a corrente com o tempo no circuito!
E aí! Como fazemos isso? 🤔🤔
Para obter essa equação, vamos aplicar a ideia de análise de malhas na malha que se forma entre os capacitores e o resistor.
Com a equação obtida, podemos obter a função corrente do circuito.
Bora começar? 😁
Passo 2
Na análise de malhas, fazemos com que a soma das tensões de uma malha é igual a .
O nosso novo circuito, desconsiderando os componentes desnecessários, é dado por
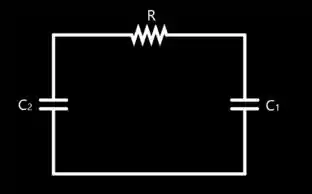
A tensão no resistor, é obtido a partir da lei de ohm . Já nos capacitores a tensão é obtida por . Ou seja, iniciando a equação, vamos obter
Perceba que as tensões são negativas pois os componentes são consumidores de energia, não geradores...
Continuando substituindo os valores, sendo e as cargas nos capacitores e , respectivamente.
Como , temos
Multiplicando por ...
Dividindo os dois lados por
Tranquilo até aqui? 👀
Passo 3
Podemos desenvolver um pouco mais essa equação
Pela conservação de energia entre os capacitores, podemos dizer que onde é a carga inicial em . Portanto
E que toda a carga que sai de para passa por , logo .
Fazendo essas substituições...
Organizando um pouquinho...
Assim, a carga EDO que gera a função carga no capacitor é
E como a variação da carga no tempo é igual a corrente, ou seja, , logo
E essa é a função que descreve a corrente no circuito!
Fim! Iae, o que achou? Responde Aí! 😁
