2CH de Física 3 da UFRJ - 2018.2

A figura abaixo mostra duas espiras condutoras circulares, concêntricas e coplanares. A espira menor possui raio e transporta uma corrente estacionária de intensidade no sentido indicado, enquanto a espira maior possui raio e transporta uma corrente estacionária de intensidade no sentido oposto.

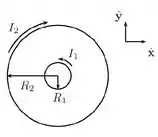
1. Determine o campo magnético resultante produzido pelas duas espiras no centro delas.
2. Suponha agora que , de forma que podemos considerar que o campo magnético produzido pela espira maior é constante em todos os pontos dentro da espira menor e tem o valor calculado no centro. Nessa situação, determine a indutância mútua entre este par de espiras.

Uma espira circular condutora, de raio e resistência elétrica gira com velocidade angular constante em torno do eixo de um sistema de coordenadas, como mostrado na figura abaixo. Ela está imersa em uma região de campo magnético constante . Considere que, no instante , a espira encontra-se sobre o plano , com seu centro sobre a origem e com o vetor unitário normal ao seu plano apontando no mesmo sentido do campo.

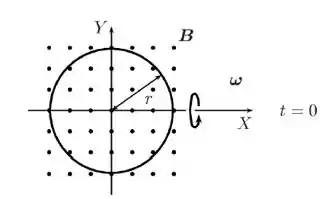
1. Determine o fluxo magnético através da área da definida pela espira em um instante qualquer.
2. Determine a corrente induzida sobre a espira no mesmo instante.
3. Determine o torque que o campo magnético exerce sobre a espira no mesmo instante.

Um semianel fino, isolante, de raio é posicionado sobre os dois primeiros quadrantes do plano de um sistema de coordenadas com seu centro sobre a origem, como mostrado na figura abaixo. Ele encontra-se carregado com densidade linear de carga estacionária, mas não-uniforme dada por , onde é uma constante positiva e é o ângulo polar, medido a partir do eixo .

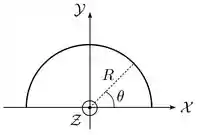
1. Determine a carga total contida no semianel.
2. Determine o vetor campo elétrico produzido pelo semianel em seu centro.

Um cilindro condutor maciço, infinito, de seção transversal circular de raio possui uma densidade superficial de carga constante e positiva. Ele se encontra em equilíbrio eletrostático.

1. Determine o vetor campo elétrico produzido pelo cilindro em um ponto a uma distância de seu eixo. Considere os casos dentro e fora do cilindro.
2. Determine o potencial elétrico produzido pelo cilindro no mesmo ponto. Considere que o potencial vale sobre a superfície do cilindro.