Listas de Física 3 - UFRJ de Física 3 da UFRJ - Lista 9 - Indutância

Um solenóide longo de raio é posicionado no interior de um segundo solenóide longo de raio , de forma que seus eixos sejam coincidentes com o eixo de um sistema de coordenadas cartesianas. O número de espiras por unidade de comprimento em cada solenóide vale e , respectivamente. Suponha que os solenóides podem ser tratados como infinitos e que o enrolamento dos fios é compacto. Quando conveniente, considere um segmento de solenóide de comprimento nas análises.

Determine a intensidade do campo magnético produzido pelo solenóide maior em seu interior, quando ele é atravessado por uma corrente estacionária de intensidade .

Um solenóide longo de raio é posicionado no interior de um segundo solenóide longo de raio , de forma que seus eixos sejam coincidentes com o eixo de um sistema de coordenadas cartesianas. O número de espiras por unidade de comprimento em cada solenóide vale e , respectivamente. Suponha que os solenóides podem ser tratados como infinitos e que o enrolamento dos fios é compacto. Quando conveniente, considere um segmento de solenóide de comprimento nas análises.

Determine a auto-indutância por unidade de comprimento do solenóide externo.

Um solenóide longo de raio é posicionado no interior de um segundo solenóide longo de raio , de forma que seus eixos sejam coincidentes com o eixo de um sistema de coordenadas cartesianas. O número de espiras por unidade de comprimento em cada solenóide vale e , respectivamente. Suponha que os solenóides podem ser tratados como infinitos e que o enrolamento dos fios é compacto. Quando conveniente, considere um segmento de solenóide de comprimento nas análises.

Determine a indutância mútua por unidade de comprimento entre o solenóide externo e o solenóide interno.

Um solenóide longo de raio é posicionado no interior de um segundo solenóide longo de raio , de forma que seus eixos sejam coincidentes com o eixo de um sistema de coordenadas cartesianas. O número de espiras por unidade de comprimento em cada solenóide vale e , respectivamente. Suponha que os solenóides podem ser tratados como infinitos e que o enrolamento dos fios é compacto. Quando conveniente, considere um segmento de solenóide de comprimento nas análises.

Suponha agora que o solenóide menor seja deslocado perpendicular ao seu eixo por uma distância . Determine a indutância mútua do sistema nessa nova configuração.

Um cabo coaxial é formado por um cilindro circular reto, condutor, maciço, de raio e uma casca cilíndrica condutora de raio , coaxial ao cilindro. Uma corrente estacionária de intensidade flui ao longo do eixo do cilindro, uniformemente distribuída sobre sua seção transversal, e uma corrente estacionária de mesma intensidade flui ao longo da casca cilíndrica, em sentido oposto à do cilindro.

Utilizando a lei de Ampère, determine a intensidade do campo magnético no interior da região entre o cilindro e a casca, ou seja, para , onde é a distância ao eixo do cilindro.

Um cabo coaxial é formado por um cilindro circular reto, condutor, maciço, de raio e uma casca cilíndrica condutora de raio , coaxial ao cilindro. Uma corrente estacionária de intensidade flui ao longo do eixo do cilindro, uniformemente distribuída sobre sua seção transversal, e uma corrente estacionária de mesma intensidade flui ao longo da casca cilíndrica, em sentido oposto à do cilindro.

Calcule o fluxo de campo magnético através de uma superfície retangular com dois lados paralelos à direção radial, se estendendo por toda a região do item anterior, e dois lados paralelos ao eixo do cabo, de comprimento .

Um cabo coaxial é formado por um cilindro circular reto, condutor, maciço, de raio e uma casca cilíndrica condutora de raio , coaxial ao cilindro. Uma corrente estacionária de intensidade flui ao longo do eixo do cilindro, uniformemente distribuída sobre sua seção transversal, e uma corrente estacionária de mesma intensidade flui ao longo da casca cilíndrica, em sentido oposto à do cilindro.

A partir do resultado acima, determine a auto-indutância por unidade de comprimento deste cabo.

Considere o mesmo cabo coaxial da questão anterior.

Utilizando o campo calculado na questão anterior, determine a densidade de energia na região entre o cilindro e a casca.

Considere o mesmo cabo coaxial da questão anterior.

Obtenha a energia total armazenada pelo campo magnético em uma porção de comprimento desta região. Sugestão: utilize como elemento de volume para integração uma casca cilíndrica de raio e espessura infinitesimal ds.

Considere o mesmo cabo coaxial da questão anterior.

A partir do resultado acima, obtenha a auto-indutância por unidade de comprimento deste cabo. Compare com o resultado obtido na questão anterior.

Considere um solenóide toroidal de raio médio , com seção transversal de área e voltas de fio enroladas de forma compacta ao longo de seu comprimento.

Utilizando a lei de Ampère, determine a intensidade do campo magnético a uma distância da origem (eixo do toróide). Assuma que as linhas de campo no interior do solenóide são circulares (e de fato são, mesmo nessa situação arbitrária).

Considere um solenóide toroidal de raio médio , com seção transversal de área e voltas de fio enroladas de forma compacta ao longo de seu comprimento.

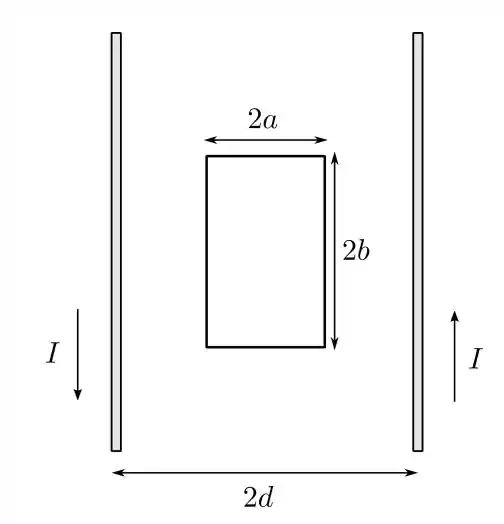
Suponha que o solenóide é fino, de forma que as dimensões de sua seção transversal sejam pequenas em comparação com . Assim, podemos dizer que o campo magnético é aproximadamente uniforme sobre a seção transversal e coincide com o valor calculado para . Nessas condições, determine a auto-indutância do sistema.

Uma espira condutora retangular de lados e é posicionada no mesmo plano que um par de fios condutores finos, retilíneos e paralelos, como mostrado na figura abaixo. Os fios transportam correntes estacionárias de mesma intensidade e sentidos opostos e estão separadas por uma distância , como indicado. O centro da espira está equidistante dos fios e os lados de comprimento são paralelos a eles. Determine a indutância mútua entre a espira e o par de fios.

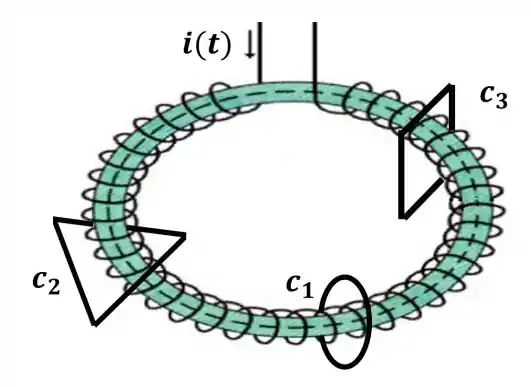
Considere um solenóide toroidal de seção transversal circular de raio . Ele é atravessado por uma corrente de intensidade que varia lentamente com o tempo. Considere também três espiras planas orientadas paralelamente às seções transversais do solenóide: , uma espira circular de raio , , uma espira triangular de lados iguais a e , uma espira quadrada de lado , dispostas no solenóide como mostrado na figura abaixo, envoltas e centralizadas no mesmo. Sejam , e as indutâncias mútuas entre o solenóide e as espiras , e , respectivamente, quando consideradas individualmente. Ordene , e de acordo com os seus módulos.

Dizemos que dois indutores de auto-indutâncias e e indutância mútua desprezível estão ligados em série quando uma mesma corrente atravessa os dois.

Calcule a diferença de potencial entre os terminais de associação. Expresse-a em termos de e e a taxa de variação de com o tempo .

Dizemos que dois indutores de auto-indutâncias e e indutância mútua desprezível estão ligados em série quando uma mesma corrente atravessa os dois.

Mostre que esse arranjo pode ser substituído por um único indutor equivalente de auto-indutância e determine em termos de e .

Dizemos que dois indutores de auto-indutância e e indutância mútua desprezível estão ligados em paralelo quando eles estão submetidos à mesma diferença de potencial elétrico .

Calcule a taxa de variação da corrente total com o tempo. Expresse-a em termos de , e .

Dizemos que dois indutores de auto-indutância e e indutância mútua desprezível estão ligados em paralelo quando eles estão submetidos à mesma diferença de potencial elétrico .

Mostre que esse arranjo pode ser substituído por um único indutor equivalente de auto-indutância e determine em termos de e .