Um semianel fino, isolante, de raio é posicionado sobre os dois primeiros quadrantes do plano de um sistema de coordenadas com seu centro sobre a origem, como mostrado na figura abaixo. Ele encontra-se carregado com densidade linear de carga estacionária, mas não-uniforme dada por , onde é uma constante positiva e é o ângulo polar, medido a partir do eixo .

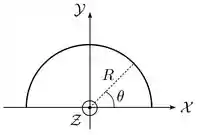
1. Determine a carga total contida no semianel.
2. Determine o vetor campo elétrico produzido pelo semianel em seu centro.

b) A primeira coisa que a gente deve reparar aqui é que a distribuição de cargas é positiva quando cosseno é positivo e negativa quando ele é negativo, já que . O cosseno é positivo entre e e negativo entre e . Isso é importante porque cada porção dessa gera um campo elétrico com características diferentes.

Vamos considerar a figura abaixo, em que desenhamos dois elementos de mesmo tamanho, mas nas posições angulares e .

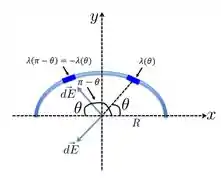
Nesse caso, o elemento que está no primeiro quadrante ( entre e ) tem carga positiva e o campo  que ele gera é de afastamento, enquanto que o outro elemento do segundo quadrante, que tem carga negativa e de mesmo módulo que a do primeiro, gera um campo  de aproximação e ambos fazem um ângulo com a direção , como indicado na figura acima.

Disso, vemos que as componentes desses campos na direção se cancelam, restando apenas uma componente que está ao longo da direção e sentido de .

Para encontrar o campo elétrico, só precisamos somar as componentes desses campos na direção .

Por isso, precisamos apenas considerar a componente ao longo de :

Agora, integrando essa expressão e lembrando que (relação fornecida no cabeçalho da prova), vamos obter que:

que vai dar os seguintes resultados

Assim

Um aspecto interessante de a gente perceber aqui é que, apesar de a carga total ser zero, como mostramos no item a), o campo elétrico resultante que o semianel produz é diferente de zero!!