P1 de Física 3 da UFRJ - 2019.1

Um grão de poeira tem a forma de uma esfera de raio igual a . Ele possui uma carga negativa uniformemente distribuída sobre seu volume, de forma que o potencial elétrico em sua superfície vale . Considerando que o potencial é nulo em um ponto infinitamente afastado do grão e que , podemos afirmar que a carga total do grão e a intensidade do campo elétrico em sua superfície valem, respectivamente:

(a) e

(b) e

(c) e

(d) e

(e) C e

(f) e

A figura abaixo mostra as linhas do campo eletrostático produzido por um par de partículas de cargas e . A figura mostra ainda duas superfícies imaginárias e fechadas, e , indicadas pelas linhas tracejadas. A superfície envolve apenas a partícula de carga , enquanto envolve as duas partículas. Considere que o vetor normal a estas superfícies aponta para fora delas, seguindo a orientação usual. Sobre essa situação, considere as afirmativas abaixo:

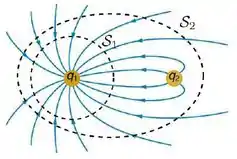
(I) O fluxo de campo eletrostático através de vale .

(II) O fluxo de campo eletrostático através de é negativo.

(III) O fluxo de campo eletrostático através de é nulo.

São VERDADEIRAS as afirmativas:

(a) Apenas I

(b) Apenas II

(c) Apenas III

(d) Apenas I e II

(e) Apenas I e III

(f) Apenas II e III

(g) I, II e III

(h) Nenhuma delas

Uma esfera condutora maciça de raio encontra-se carregada com uma carga total . Ela está envolvida por uma casca esférica isolante de raio interno e raio externo (), uniformemente carregada com uma densidade volumétrica de carga , como mostrado na figura abaixo. A esfera e a casca são concêntricas e o sistema se encontra em equilíbrio eletrostático.

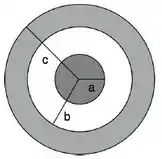
Utilizando a lei de Gauss, determine o vetor campo elétrico produzido pelo sistema em um ponto a uma distância r do centro da esfera. Considere todas as regiões distintas do espaço, dadas por

(i); (ii) ; (iii) ; e (iv) .

Justifique cuidadosamente todos os argumentos utilizados.

A figura abaixo mostra duas distribuições de carga isoladas. Na esquerda, um anel circular fino, isolante, de raio , encontra-se uniformemente carregado e possui uma carga total . Na direita, uma coroa circular fina, isolante, de raio interno e raio externo encontra-se uniformemente carregada com uma densidade superficial de carga . Em ambas as situações, considere que o potencial elétrico produzido por cada uma das distribuições é nulo em um ponto infinitamente afastado delas. Considere ainda que o eixo é perpendicular ao plano definido por cada distribuição e passa pelo centro delas.

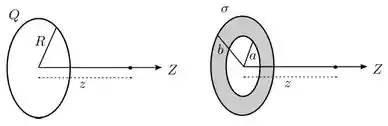
(a) Determine o potencial elétrico produzido pelo anel em um ponto sobre o eixo, localizado a uma distância do centro do anel.

(b) Determine o potencial elétrico produzido pela coroa em um ponto sobre o eixo , localizado a uma distância do centro da coroa.

Sugestão: Divida a coroa em aneis infinitesimais concêntricos e utilize o resultado do item anterior.

(c) Obtenha uma expressão assintótica para o potencial encontrado no item (b) no limite em que o ponto está muito distante do centro da coroa, de forma que. Interprete o resultado.

Considere um plano infinito, uniformemente carregado, coincidente com o plano de um dado sistema de coordenadas. Sobre o campo elétrico produzido por este plano, considere as afirmativas abaixo:

(I) é independente das coordenadas e .

(II) A direção de é paralela ao eixo em todos os pontos do espaço.

(III) aponta no mesmo sentido em todos os pontos do espaço.

São VERDADEIRAS as afirmativas:

(a) Apenas I e II

(b) Apenas I

(c) Apenas II

(d) Apenas III

(e) Apenas I e III

(f) Apenas II e III

(g) I, II e III

(h) Nenhuma delas

Na figura abaixo, as linhas pontilhadas representam algumas superfícies equipotenciais de uma distribuição de cargas esfericamente simétrica com carga total positiva. Uma partícula de carga positiva pode ser deslocada do ponto até alguns possíveis pontos finais indicados na figura. O deslocamento é feito por meio das trajetórias , , e indicadas. Sobre o trabalho realizado pela força elétrica que atua sobre a partícula ao longo dessas trajetórias (,, e , respectivamente), é CORRETO afirmar que:

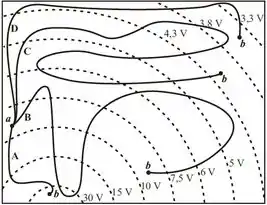
(a)

(b)

(c)

(d)

(e)

(f)

(g)

Quatro partículas carregadas são fixadas sobre os vértices de um quadrado de lado , como mostrado na figura abaixo. Duas delas possuem carga e as outras duas possuem carga . Este quadrado encontra-se sobre o plano , com seu centro sobre a origem e seus lados paralelos aos eixos e . O eixo é perpendicular ao plano do quadrado e passa por seu centro. Sobre essa situação, assinale a alternativa CORRETA:

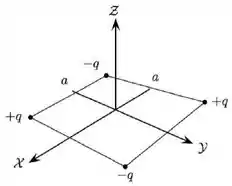
(a) O trabalho realizado pela força elétrica ao trazer as quatro partículas do infinito até a configuração indicada na figura é nulo.

(b) O campo elétrico resultante produzido pelas quatro partículas tem a mesma intensidade em todos os pontos do eixo .

(c) O campo elétrico resultante produzido pelas quatro partículas é nulo em todos os pontos do eixo .

(d) A força elétrica resultante sobre qualquer uma das partículas devido às outras três é nula.

(e) Uma partícula carregada abandonada do repouso sobre o centro do quadrado entrará em movimento devido à ação de uma força elétrica.

Considere os dois circuitos mostrados na figura abaixo. Todos os capacitores são idênticos e tem capacitâncias iguais a . A diferença de potencial entre os terminais e também é a mesma. Sejam e as capacitâncias equivalentes dos circuitos 1 e 2 entre os terminais e , respectivamente. Nessa situação, podemos afirmar que a razão vale:

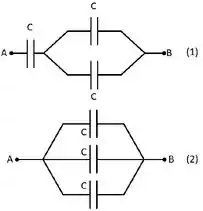
(a)

(b)

(c)

(d)

(e)

(f)

(g)