Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Lenz

Ver Teoria
Exercício 36123456789101112131415161718192021222324252627282930313233343537383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697

Enunciado

UFRJ- Física 3 – SC 2018.2 - DIURNO - 4

Uma espira circular condutora, de raio r e resistência elétrica R gira com velocidade angular constante ω em torno do eixo X de um sistema de coordenadas, como mostrado na figura abaixo. Ela está imersa em uma região de campo magnético constante  B → = B   z ^   ( B > 0 ) . Considere que, no instante t = 0 , a espira encontra-se sobre o plano X Y , com seu centro sobre a origem e com o vetor unitário normal ao seu plano apontando no mesmo sentido do campo.

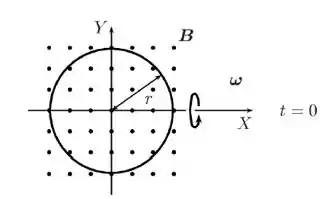
  1. Determine o fluxo magnético através da área da definida pela espira em um instante t qualquer.
  2. Determine a corrente induzida sobre a espira no mesmo instante.
  3. Determine o torque que o campo magnético exerce sobre a espira no mesmo instante.

Passo 1

a) Vamos considerar que a normal do plano  n ^ faz um ângulo θ ( t ) com o campo magnético  B → . Como a velocidade angular é constante, esse ângulo é dado por

θ t = θ 0 + ω t   ,  

em que θ 0 = θ ( t = 0 ) é o ângulo inicial que  n ^ faz com  B → . No caso do problema, como a espira está inicialmente no plano X Y , então θ t = 0 = 0 .

Portanto,

θ t = ω t   .

Como B → é constante, isso significa que ele tem o mesmo valor em todos os pontos da superfície da espira e também não varia com o tempo. Além disso, para todo instante de tempo t , o ângulo θ ( t ) entre  n ^ e  B → tem o mesmo valor em todos os pontos da superfície da espira, já que a superfície da espira é plana.

Com isso, a gente consegue calcular o fluxo magnético, que vai ser dado por

Φ B ( t ) = ∫ S B → ⋅ d A → = B → ⋅ A →

Aonde esse produto escalar é dado por:

B → ⋅ A → = B A c o s θ

E substituindo o valor do ângulo que encontramos a pouco, teremos:

Φ B t = B A c o s ω t

Passo 2

b) Como o fluxo magnético varia com o tempo, vai aparecer uma fem induzida na espira, que é dada por

ε = - d Φ B t d t

Derivando esse fluxo com relação ao tempo, vamos ter:

d d t B A c o s ω t

Aqui temos uma regra da cadeia por conta da função cosseno, aonde teremos a derivada do que está dentro, vezes a derivada da função:

d d t cos ⁡ ω t = ω × - s e n ( ω t )

d d t cos ⁡ ω t = - ω s e n ( ω t )

E por fim, a derivada completa vai ser:

d d t B A c o s ω t = - B A ω s e n ω t

Substituindo na expressão da fem induzida:

ε = - - B A ω s e n ω t

ε = B A ω s e n ω t

E sabendo que essa área, é uma área circular com raio r conhecido, temos:

A = π r 2

Substituindo:

ε = B π r 2 ω s e n ( ω t )

Encontramos a fem induzida na espira, para fechar precisamos encontrar a corrente induzida, e para isso, conhecendo a resistência R da espira, vamos aplicar a lei de Ohm.

ε = R I i n d

ω B π r 2 sen ⁡ ω t = R I i n d    

I i n d = ω B π r 2 sen ⁡ ω t R   .

Passo 3

c) Como o campo magnético é uniforme, então podemos utilizar a seguinte expressão para o torque   τ →

τ → = μ → × B →   .

O momento de dipolo magnético é   μ → = I i n d   A → = I i n d π r 2   n ^ . Como   B → = B   z ^ , então teremos

τ → = I i n d π r 2 B n ^ × z ^

Substituindo I i n d

τ → = ω B π r 2 sen ⁡ ω t R π r 2 B n ^ × z ^

τ → = ω B π r 2 2 sen ⁡ ω t R n ^ × z ^

Agora, para fechar, temos que notar que o ângulo   n ^ e   z ^ varia com o tempo e vale θ t = ω t . Por isso, vamos ter que  n ^ × z ^ = - sen ⁡ ω t x ^ .Substituindo na expressão para o torque

τ → = ω B π r 2 sen ⁡ ω t 2 R - x ^

Resposta

  1. Φ B t = ω B π r 2 cos ⁡ ω t
  2. I i n d = ω B π r 2 sen ⁡ ω t R   ;
  3. τ → = ω B π r 2 sen ⁡ ω t 2 R - x ^

Exercícios de Livros Relacionados

20- Uma barra metálica com 1.50m de comprimento é puxada para a direita a 5.0m / s regulares e perpendicularmente a um campo magnético uniforme de 0.750T . A barra desliza sobre trilhos metálicos para
17- Use a lei de Lenz para determinar o sentido da corrente induzida que passa no resistor a b indicado na Figura 29.33 , quando ( a ) a chave S é aberta depois de ficar fechada durante alguns minutos
15- Um anel circular está em uma região do espaço onde existe um campo magnético uniforme, como indica a Figura 29.31 . O campo magnético está entrando no plano da figura. Determine o sentido (horário
18- Um tubo de papelão é circundado por dois enrolamentos feitos com dois fios isolados, formando espiras em sentidos contrários, como indica a Figura 29.34 . Os terminais a e b do enrolamento A podem
16- A corrente na Figura 29.32 obedece a equação I t = I 0 e - b t . Em que b0 . Determine o sentido (horário ou anti-horário) da corrente induzida na bobina redonda para t0 .