P1 de Física 3 da UFRJ - 2011.1

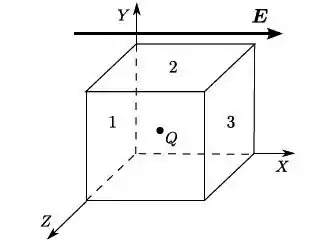
Numa região do espaço de interesse, existe um campo elétrico constante (uniforme e estacionário), na direção e sentido de . Nessa mesma região, temos uma superfície cúbica abstrata, que encerra uma partícula (pontual) de carga localizada no seu centro. Três das faces do cubo estão assinaladas na figura: as faces e são paralelas ao plano , ao passo que a face é paralela ao plano . Em relação ao fluxo (, , ) do campo elétrico através de cada uma dessas faces (com orientação do vetor normal para fora, como usual), qual das alternativas abaixo é a correta?

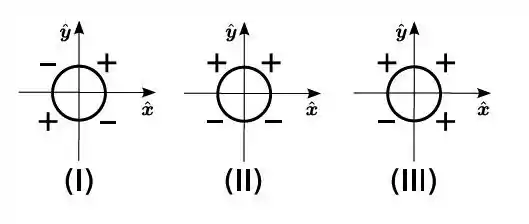
Três anéis circulares, de mesmo raio, cujos quadrantes foram carregados uniformemente com cargas positivas e negativas, de mesmo módulo, estão representados na figura abaixo. Considere as seguintes afirmações: (A) o campo elétrico no centro do anel I é nulo; (B) o campo elétrico no centro do anel II tem direção e sentido de ; (C) o campo elétrico no centro do anel III tem direção e sentido de .

1. Somente a afirmação A está correta.
2. Somente a afirmação B está correta.
3. Somente a afirmação C está correta.
4. Somente as afirmações A e B estão corretas.
5. Somente as afirmações A e C estão corretas.
6. Somente as afirmações B e C estão corretas
7. Todas as três afirmações (A, B e C) estão corretas.

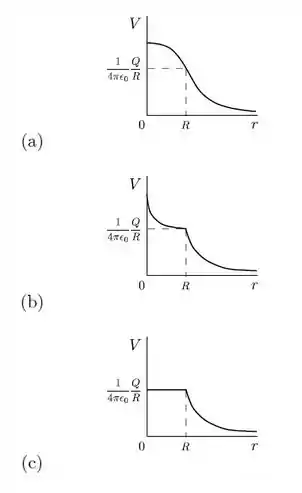
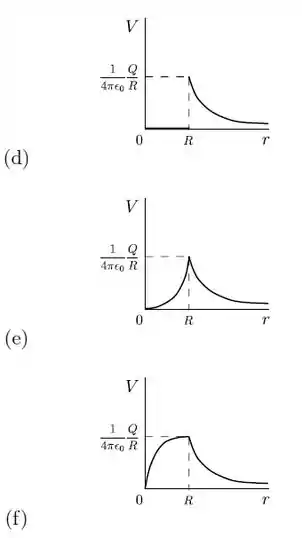
Qual dos gráficos abaixo melhor representa o potencial eletrostático de uma esfera de raio e carga uniformemente distribuída em todo o seu interior, supondo o potencial zero no infinito?

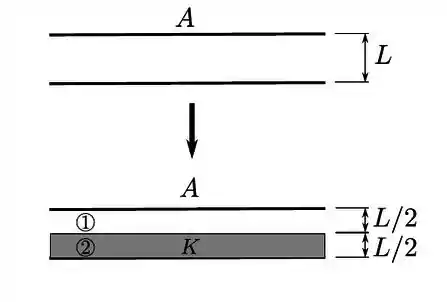
Um capacitor de placas planas e paralelas, de área , a distância , é “recheado” por uma chapa condutora, também de área , e espessura .

A capacitância de tal capacitor é:

Um capacitor plano-paralelo tem placas idênticas de área , cada uma, com separação entre elas (conforme parte superior da figura ao lado). Numa primeira etapa, tal capacitor é ligado a uma bateria até atingir um módulo de diferença de potencial entre suas placas e, imediatamente, desconectado da bateria.

1. Determine o módulo do campo elétrico e a energia eletrostática armazenada

Numa segunda etapa um isolante de constante dielétrica é inserido no capacitor, preenchendo pela metade região entre suas placas, conforme mostrado na parte inferior da figura ao lado.

2. Determine o módulo da nova diferença de potencial entre as placas.
3. Determine o módulo (, , ) do novo campo elétrico em cada uma das duas “metades” ( e ) entre as placas.
4. Determine a nova energia eletrostática armazenada .

Duas esferas condutoras, carregadas, de raios e estão afastadas a uma distância muito grande, de modo que o campo elétrico na vizinhança de cada esfera pode ser considerado como somente devido à distribuição de carga uniforme da própria esfera. As esferas estão ligadas por um fio condutor fino que simplesmente promove o contato elétrico entre elas. Se , qual é a afirmação verdadeira?

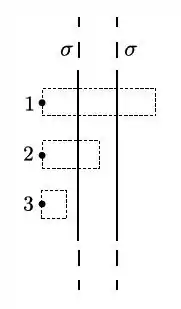
A figura representa o perfil de uma placa condutora de espessura finita e demais dimensões muito maiores que . A densidade superficial de carga em ambas as faces da placa é constante (uniforme e estacionária). Considerando as três superfícies cilíndricas indicadas na figura, qual das afirmativas abaixo é correta?

Qual das seguintes afirmativas é falsa?

1. No processo de carregamento de um capacitor, cria-se um campo elétrico entre suas placas.
2. O trabalho necessário para se carregar um capacitor pode ser pensado como o trabalho necessário para se criar um campo elétrico entre suas placas
3. A densidade de energia na região entre as placas de um capacitor depende linearmente do módulo do campo elétrico
4. A diferença de potencial entre as placas de um capacitor plano paralelo depende linearmente do módulo do campo elétrico
5. Ao dobrarmos a carga em cada uma das placas de um capacitor dado, dobramos a diferença de potencial entre suas placas

Duas partículas (pontuais), separadas por uma distância , com cargas elétricas e diferentes (), produzem um potencial nulo num ponto do espaço. Tomando o potencial como zero no infinito, isso significa necessariamente que:

1. Não há outra força elétrica atuando sobre uma outra partícula de teste colocada no ponto
2. As cargas e devem ter o mesmo sinal
3. O trabalho para colocar a partícula de carga a uma distância da partícula de carga é zero
4. O trabalho para trazer uma partícula de teste carregada, desde o infinito até o ponto , é zero

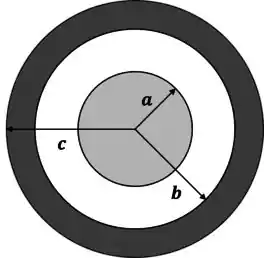
Uma esfera sólida metálica de raio e uma casca esférica bidimensional, de raio são concêntricas e estão, cada uma, em equilíbrio eletrostático (sem contato). Na esfera interna, existe uma carga , qao passo que, na casca externa, existe uma carga . Qual das afirmativas abaixo corresponde ao potencial eletrostático desse sistema nas regiões:

Considere o potencial como zero no infinito.

Temos três distribuições não homogêneas de carga: I1) uma distribuição linear num fio de comprimento , cuja densidade linear de carga é: (); (2) Uma distribuição superficial sobre um disco de raio , cuja densidade superficial é: (); (3) Uma distribuição volumétrica numa esfera de raio , cuja densidade volumétrica é: (). Aqui, (, , ) são constantes. A carga total de cada uma dessas três distribuições é a mesma, . Qual das alternativas é a correta?

1. ; ;
2. ; ;
3. ; ;
4. ; ;
5. ; ;
6. ; ;

Uma esfera, de raio e carga total , possui uma densidade volumar (resultante) de carga estacionária, mas não uniforme, dada por:

Onde é uma constante e é a distância até o seu centro. Essa esfera está envolta por uma casca esférica condutora, concêntrica, de raio interno e raio externo , com carga total , em equilíbrio eletrostático.

1. Expresse a constante como função de e de .
2. Quais são as densidades superficiais de carga na casca esférica condutora?
3. Determine o campo elétrico nas quatro regiões:
4. Determine o potencial eletrostático nas quatro regiões supracitadas, tomando-o como zero no infinito.