PF de Física 3 da UFRJ - 2018.1 - Diurno
Física 3 - UFRJ
Uma placa condutora, de lado e espessura desprezível possui uma carga uniformemente distribuída sobre sua superfície. Considere um ponto sobre o eixo perpendicular ao plano da placa e que passa por seu centro, a uma distância do mesmo. Se este ponto está muito próximo da placa, de forma que , a intensidade do campo elétrico produzido pela placa neste ponto vale, aproximadamente:
Sobre um condutor maciço em equilíbrio eletrostático, considere as afirmativas abaixo:
- Se o condutor está carregado, sua superfície deve possuir um potencial elétrico diferente de seu interior.
- O campo elétrico é sempre tangente à superfície do condutor na vizinhança externa do mesmo.
- No interior do condutor, o campo elétrico deve ser necessariamente nulo.
São VERDADEIRAS as afirmativas:
- I
- II
- III
- I e II
- I e III
- II e III
- I, II e III
- Nenhuma delas.
Um fio fino, retilíneo e finito de comprimento está uniformemente carregado com uma carga total . Desenha-se então uma superfície fechada na forma de um cilindro reto de raio e comprimento , como mostrado na figura abaixo. O cilindro é posicionado de forma que seu eixo coincida com o eixo do fio e os centros de suas tampas toquem as extremidades do fio. Sobre essa situação, considere as afirmativas abaixo:
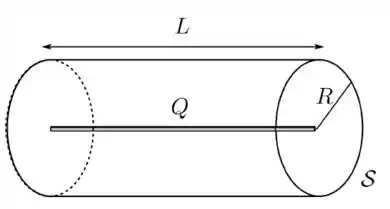
- O campo elétrico produzido pelo fio tem módulo constante em todos os pontos sobre a superfície lateral do cilindro.
- O campo elétrico produzido pelo fio é tangente a todos os pontos das tampas do cilindro.
- O fluxo de campo elétrico produzido pelo fio através de vale .
São VERDADEIRAS as afirmativas:
- I
- II
- III
- I e II
- I e III
- II e III
- I, II e III
- Nenhuma delas.
Em muitos livros-texto, é comum ver a seguinte definição de campo elétrico: seja uma pequena carga de prova positiva ; define-se o campo elétrico na região de como , onde é a força elétrica agindo sobre devido a uma distribuição de cargas qualquer. Nessa definição, está implícita que a distribuição de cargas não é afetada pela presença de . Se ao invés de uma pequena carga positiva tivéssemos utilizado uma pequena carga negativa para definir , o que se poderia dizer a respeito do campo de acordo com esta nova definição?
- O campo permaneceria com os mesmos módulo, direção e sentido da definição original.
- O campo permaneceria com os mesmos módulo e direção, porém com sentido oposto ao da definição original.
- O campo permaneceria com o mesmo módulo, porém com direção e sentido perpendiculares aos da definição original.
- O campo permaneceria com os mesmos direção e sentido da definição original, porém o módulo poderia depender do módulo de .
- Nada se pode dizer, pois o campo depende da distribuição de cargas, da qual não temos informação.
A figura abaixo mostra as linhas do campo eletrostático produzido por duas partículas de cargas e . Sobre esse sistema, podemos afirmar que:
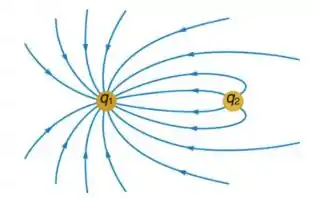
- , e
- , e
- , e
- , e
- , e
- , e
- , e
- , e
Dois capacitores idênticos, inicialmente no vácuo, são conectados aos terminais de uma bateria que fornece uma diferença de potencial constante , como mostrado na figura abaixo. A seguir, mantendo a bateria conectada, insere-se uma placa isolante de constante dielétrica entre as placas de um dos capacitores, de forma a ocupar todo o volume entre elas. Nessa situação, é correto afirmar que, após a inserção:
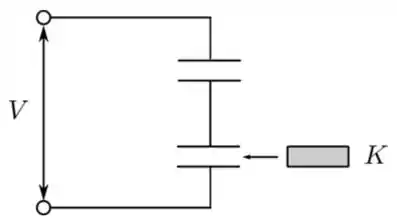
- A carga armazenada no capacitor com o dielétrico diminui com relação ao valor original.
- Os dois capacitores armazenam a mesma energia.
- A carga armazenada no capacitor que permanece no vácuo aumenta com relação ao valor original.
- Os dois capacitores terão a mesma diferença de potencial entre suas placas.
- A energia armazenada no capacitor que permanece no vácuo diminui com relação ao valor original.
Um campo magnético uniforme e estacionário aponta para dentro do plano da página. Uma partícula carregada, movendo-se no plano da página, segue uma espiral no sentido horário de raio decrescente, como mostrado na figura abaixo. Uma explicação razoável para esta trajetória é:
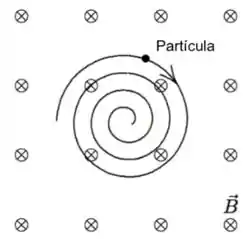
- A carga da partícula é positiva e sua velocidade está diminuindo.
- A carga da partícula é positiva e sua velocidade está aumentando.
- A carga da partícula é negativa e sua velocidade está aumentando.
- A carga da partícula é negativa e sua velocidade está diminuindo.
- Não há dados suficientes para dar uma explicação razoável.
Uma placa plana isolante, de espessura desprezível, infinita, possui densidade superficial de carga constante. Um elétron (carga ), inicialmente em repouso, é deslocado lentamente por um agente externo de uma posição inicial, cuja distância à placa é até uma posição final, cuja distância à placa é , e deixado em repouso. Qual é o trabalho realizado pelo agente externo sobre o elétron nesse percurso?
Considere uma espira retangular de lados e () e um fio retilíneo infinito, no mesmo plano da espira. Sabendo que o fio retilíneo é paralelo aos lados longos da espira e que o fio e a espira portam, respectivamente, correntes estacionárias para a direita e no sentido horário, assinale a única opção INCORRETA.
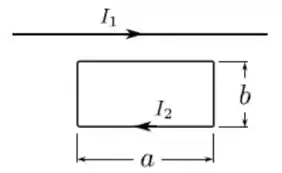
- A força sobre cada um dos lados curtos da espira é não-nula.
- A soma vetorial das forças sobre os lados curtos da espira é nula.
- A soma vetorial das forças sobre os lados longos da espira é nula.
- As forças sobre os lados longos da espira estão na mesma direção.
- A força resultante sobre a espira tem direção perpendicular ao fio retilíneo.
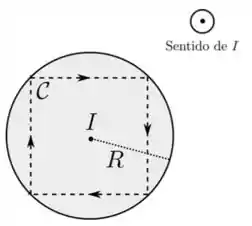
Um fio condutor retilíneo tem seção transversal circular de raio , como mostrado na figura abaixo. Uma corrente estacionária de intensidade atravessa o fio com sentido para fora do plano do papel, uniformemente distribuída sobre a seção transversal. Desenha-se então uma curva fechada e orientada na forma de um quadrado inscrito no perímetro dessa seção, com a orientação indicada. Nessa situação, podemos afirmar que a circulação do campo magnético produzido pelo fio ao longo de , dada por , vale:
Duas espiras condutoras circulares, concêntricas, encontram-se sobre um mesmo plano. A primeira espira tem raio e transporta uma corrente estacionária de intensidade . A segunda tem raio e também transporta uma corrente estacionária em sentido oposto ao da primeira. Sabendo que o campo magnético produzido pelas duas espiras é nulo no centro delas, a intensidade da corrente na segunda espira vale:
Um campo magnético uniforme atua apenas sobre uma região do espaço definida por um disco circular de raio e aponta para fora do plano do papel, como mostrado na figura abaixo. Duas partículas idênticas de carga , unidas por uma haste isolante rígida de comprimento , são posicionadas nesta região de forma que o eixo da haste é perpendicular à direção do campo e o centro dela coincide com o centro dessa região, como indicado. Sabendo que a haste encontra-se inicialmente em repouso e que a intensidade do campo magnético aumenta lentamente com o tempo, podemos afirmar que:
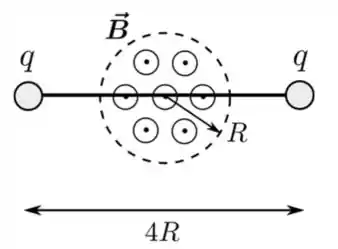
- A haste começará a girar em sentido anti-horário, devido ao torque gerado pela força elétrica.
- A haste começará a girar em sentido horário, devido ao torque gerado pela força magnética.
- A haste começará a girar em sentido anti-horário, devido ao torque gerado pela força magnética.
- A haste permanecerá em repouso, uma vez que a força resultante sobre ela é nula.
- A haste começará a girar em sentido horário, devido ao torque gerado pela força elétrica.
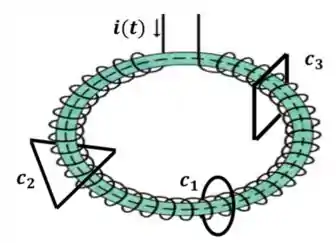
Considere um solenóide toroidal de seção transversal de raio . Ele é atravessado por uma corrente de intensidade que varia lentamente com o tempo. Considere também três espiras orientadas paralelamente às seções transversais do solenoide: , uma espira circular de raio , , uma espira triangular de lados iguais a e , uma espira quadrada de lado , dispostas no solenóide como mostrado na figura abaixo, envoltas e centralizadas no mesmo. Sejam , e as indutâncias mútuas entre o solenóide e as espiras , e , respectivamente, quando consideradas individualmente. Nessa situação, podemos afirmar que:
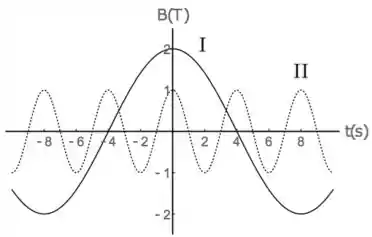
Considere duas situações: na primeira, uma espira circular de área é atravessada perpendicularmente por um campo magnético uniforme que oscila periodicamente no tempo de acordo com a curva na figura abaixo (curva cheia), e na segunda situação, a mesma espira é atravessada perpendicularmente por um campo magnético uniforme oscilante descrito pela curva (pontilhada). Podemos afirmar que a maior amplitude do fluxo de campo magnético e a maior amplitude da fem induzida ocorrem, respectivamente, nas situações
- Não é possível determinar sem conhecer a resistência elétrica da espira.