P1 de Física 3 da USP - 2018
Física 3 - USP
Considere um capacitor formado por duas cascas cilíndricas metálicas de raios (interno) e raio (externo) com cargas e , respectivamente. Ambos os cilindros são muito longos e possuem comprimento , de forma que efeitos de borda podem ser desprezados.
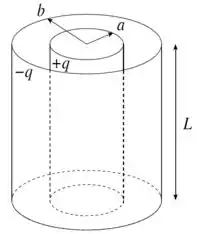
- Calcule a densidade de carga nas superfícies interna e externa do capacitor. Expresse suas respostas em termos de e das dimensões do sistema.
- Determine o vetor campo elétrico em todo o espaço.
- Determine a capacitância do capacitor.
Considere um anel com raio e espessura desprezível que está parcialmente carregado. O centro do anel coincide com a origem do sistema de coordenadas, conforme mostrado na figura abaixo e encontra-se disposto com a origem ao longo do plano . A distribuição de carga no anel é dada por:

onde é o ângulo polar e é uma constante positiva. Considere nulo o potencial elétrico no infinito.
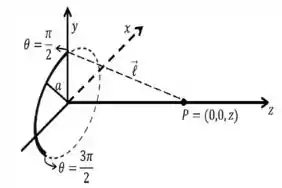
- Determine o vetor campo elétrico no ponto do eixo do anel.
- Determine o potencial elétrico no ponto do eixo do anel.
Considere uma casca esférica (não condutora) que está centrada na origem . Ela é uniformemente carregada com carga e possui raio , cujo centro situa-se à uma distância de um plano infinito, uniformemente carregado com uma densidade superficial , conforme mostrado na figura abaixo.
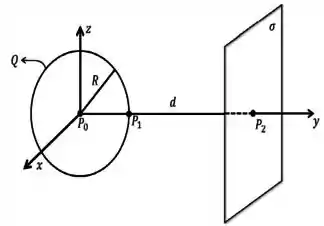
- Determine o vetor campo elétrico em todo o espaço devido à casca esférica.
- Determine o vetor campo elétrico em todo o espaço devido à carga na superfície plana.
- Determine o vetor campo elétrico resultante ao longo do eixo .
- Calcule a diferença de potencial entre os pontos e localizados na superfície plana e no centro da casca, respectivamente.
Um arranjo é formado por uma esfera condutora sólida de raio , centrada no ponto na origem, eletrizada com carga envolvida por um casca esférica condutora de raio interno e externo também eletrizada com carga , conforme ilustrado na figura abaixo:
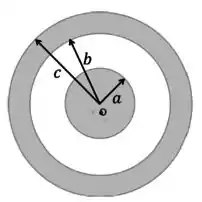
- Sendo a distância até a origem , determine o vetor campo elétrico nas regiões ,, e .
- Determine a carga em cada uma das superfícies , e na situação de equilíbrio eletrostático. Justifique sua resposta.
- Determine as densidades superficiais de carga , e .