Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Gauss – Simetrias

Ver Teoria
Exercício 631234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Usp - Física 3 – P1 2018.1 - 4

Considere um capacitor formado por duas cascas cilíndricas metálicas de raios a (interno) e raio b (externo) com cargas q > 0 e q < 0 , respectivamente. Ambos os cilindros são muito longos e possuem comprimento L , de forma que efeitos de borda podem ser desprezados.

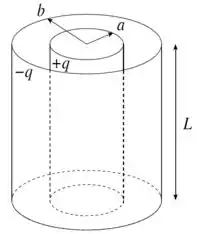
  1. Calcule a densidade de carga nas superfícies interna e externa do capacitor. Expresse suas respostas em termos de q e das dimensões do sistema.
  2. Determine o vetor campo elétrico em todo o espaço.
  3. Determine a capacitância do capacitor.

Passo 1

a) A densidade de carga nas superfícies internas e externas são dadas por

σ a = q 2 π a L     ;   σ b = - q 2 π b L   ,

respectivamente.

Passo 2

b) Adotando como superfície gaussiana S um cilindro de raio r concêntrico ao capacitor e com altura h (figura abaixo), temos que, ao longo das tampas do cilindro,    E → é perpendicular a   r ^ e, portanto, apenas a superfície lateral do cilindro contribui para o fluxo.

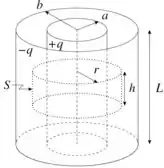
Portanto,

∮ S E → ⋅ d A → = E 2 π r h = Q i n t ϵ 0   .  

Para r < a e r > b , temos que Q i n t = 0 e Q i n t = q - q = 0 , respectivamente, de forma que o campo elétrico é nulo nessas regiões.

Para a < r < b , Q i n t = q h / L e, portanto,

E → = q 2 π ϵ 0 r L   r ^     .  

Passo 3

c) A diferença de potencial entre as superfícies interna e externa é dada por

V a - V b = - ∫ a b E → ⋅ d l → = q 2 π ϵ 0 L ln ⁡ ( b / a )

e, portanto, a capacitância do capacitor é dada por

C = q V a - V b = 2 π ϵ 0 L ln ⁡ b a     .

Resposta

  1. σ a = q 2 π a L     ;   σ b = - q 2 π b L   ;
  2. E → = q 2 π ϵ 0 r L   r ^   ;
  3. C = q V a - V b = 2 π ϵ 0 L ln ⁡ b a   .

Exercícios de Livros Relacionados

A Fig. 23-30 mostra uma superfície gaussiana com a forma de um cubo de 2,00 m de aresta, imersa em um campo elétrico dado porE → = 3,00 x + 4,00 i ^ + 6,00 j ^ + 7,00 k ^ N / C , com x em metros. Qual
Uma fina casca esférica não-condutora de raio R 1 tem carga total q 1 uniformemente distribuída em sua superfície. Uma segunda fina casca esférica não condutora e maior, de raio R 2 , coaxial com a pr
Uma esfera de raio R tem densidade volumétrica de carga ρ = B / r para rR , onde B é uma constante e ρ = 0 para rR . (a) Determine a carga total na esfera. (b) Determine as expressões par ao campo elé
Um cilindro sólido não condutor infinitamente longo de raio a tem uma massa específica volumétrico uniforme de ρ 0 . Mostre que o campo elétrico é dado pelas seguintes expressões: E R = ρ R / 2 ε 0 pa
Uma fina casca cilíndrica de comprimento 200m e raio 6,00c m tem uma densidade superificial uniforme de carga de 9,00n C / m 2 . (a) Qual é a carga total na casca? Determine o campo elétrico nas segui