P2 de Física 3 da USP - 2018

Um circuito condutor é composto por dois fios retilíneos semi-infinitos e uma parte circular, representados pelas linhas escuras, conforme mostrado na figura abaixo. Ele está contido no plano e conduz uma corrente no sentido indicado. Para e os trechos são retilíneos (fios semi-infinitos). Para e , o condutor tem a forme de três quartos de circunferência com raio .

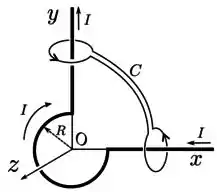
1. Calcule o vetor campo magnético   na origem devido aos segmentos lineares do fio.
2. Calcule o vetor campo magnético   na origem do sistema de coordenadas devido à parte circular.
3. Determine o valor da integral ao longo do percurso indicado na figura.

Um material condutor de condutividade uniforme tem o formato de um semi-círculo de altura e raios e , conforme indicado nas figuras e , respectivamente. As superfícies localizadas em e são equipotenciais e mantidas a uma diferença de potencial por uma bateria. Vamos assumir que o potencial elétrico dentro do condutor depende somente da coordenada , de forma que os efeitos de borda podem ser desprezados.

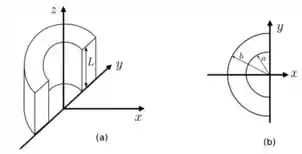
1. A bateria fornece uma corrente elétrica . Assumindo a conservação de corrente, determine o vetor densidade de corrente  .
2. Determine o campo elétrico   no interior do condutor.
3. Calcule a resistência do condutor em função de sua condutividade e de suas dimensões.

Uma espira triangular, de base e altura , contida no plano , é percorrida por uma corrente no sentido horário, conforme a figura abaixo. Na região onde se encontra a espira, existe um campo magnético

onde é uma constante.

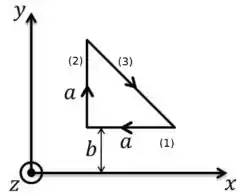
1. Calcule o vetor força magnética sobre os lados 1 e 2 da espira.
2. Calcule o vetor força magnética sobre o lado 3 da espira.
3. Determine o vetor momento de dipolo magnético e o vetor força resultante sobre a espira.

Considere um fio retilíneo muito longo de raio e centrado ao longo do eixo no qual passa uma corrente estacionária (ao longo da direção ), conforme mostra a figura abaixo. A corrente elétrica é distribuída de forma que sua densidade de corrente é dada por:   (se ), e caso contrário, sendo uma constante.

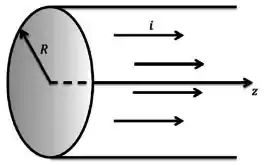
1. Determine a corrente total em função de e .
2. Usando a lei de Ampère, encontre o vetor campo magnético   na região .
3. Usando a lei de Ampère, encontre o vetor magnético   na região .