P3 de Física 3 da USP - 2016

Um feixe de luz laser monocromático incide normalmente sobre uma placa que absorve totalmente a radiação. O feixe tem intensidade e seção reta circular de raio .

(a) Calcule a amplitude do campo magnético do feixe.

(b) Calcule a energia média absorvida pela placa no intervalo de tempo .

(c) Calcule a energia eletromagnética média contida num comprimento do feixe.

Considere um sistema composto por um fio retilíneo infinito e uma espira quadrada de lado . O fio, que está colocado ao longo do eixo de um sistema de referência, é percorrido por uma corrente e gera um campo magnético dado por , onde é a distância até o fio.

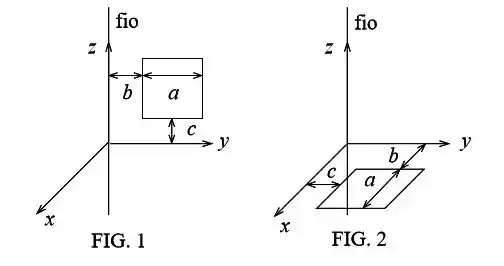
(a) Calcule a indutância mútua entre o fio e a espira quando ela está colocada no plano , conforme a figura .

(b) Calcule a indutância mútua entre o fio e a espira quando ela está colocada no plano , conforme a figura .

(c) Suponha, agora, que a espira tem resistência e que a corrente no fio varia no tempo como , onde é uma constante positiva. Com a espira na posição indicada na figura , calcule a corrente induzida na espira. Esta corrente circula a espira no sentido horário ou anti-horário? Justifique sua resposta.

Uma onda eletromagnética plana monocromática de comprimento de onda propaga-se no vácuo no sentido positivo do eixo . Seu campo elétrico oscila na direção e sua amplitude assume metade do seu valor máximo na origem do sistema de coordenadas no instante . Nos itens (a) e (b) abaixo, expresse suas respostas em termos de , , e .

(a) Escreva as expressões dos vetores campo elétrico e campo magnético associados a esta onda.

(b) Calcule o vetor Poynting.

(c) No instante , um elétron de carga está passando pela origem do sistema de coordenadas com velocidade , na direção e sentido do eixo . Calcule o vetor força que age sobre o elétron em devido a essa onda.

(I) Um capacitor de placas paralelas circulares, no vácuo, está sendo carregado, como indica a figura abaixo. As placas têm raio e a corrente de condução nos fios no instante é igual a .

Calcule o campo magnético no ponto a uma distância do eixo do capacitor, conforme a figura. Dado: o campo elétrico dentro do capacitor é , onde é a densidade superficial de carga.

(II) O campo elétrico de uma onda que se propaga no vácuo é dada por , onde a constante . Use a lei de Faraday, , para calcular o campo vetorial desta onda.