Considere um anel com raio e espessura desprezível que está parcialmente carregado. O centro do anel coincide com a origem do sistema de coordenadas, conforme mostrado na figura abaixo e encontra-se disposto com a origem ao longo do plano . A distribuição de carga no anel é dada por:

onde é o ângulo polar e é uma constante positiva. Considere nulo o potencial elétrico no infinito.
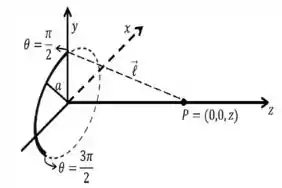
- Determine o vetor campo elétrico no ponto do eixo do anel.
- Determine o potencial elétrico no ponto do eixo do anel.
Passo 1
- Para vermos como calcular o campo elétrico nesse caso, considere a figura abaixo, em que rotacionamos a figura do enunciado só para facilitar a visualização dos vetores. Nela, o vetor e localizam, respectivamente, o ponto e o elemento de carga que produz o campo em .
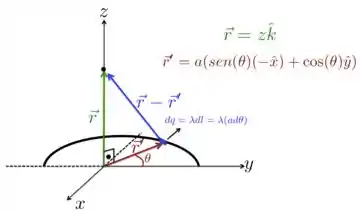
Um detalhe importante é: como eu rotacionei a figura o intervalo de ângulo onde eu tenho carga é . Se não tivesse rotacionado a figura o vetor seria e o intervalo seria .
Como ’ é o vetor unitário que indica a direção de e , podemos representar o campo como:
De acordo com a figura, podemos escrever o vetor unitário da seguinte forma:
em que também utilizamos que , que podemos tirar do triângulo retângulo da figura acima. Colocando tudo isso junto em , temos:
Agora, como a distância ao ponto é fixa para todo ângulo, o campo total pode ser escrito como:
Lembrando que como eu rotacionei a figura o intervalo mudou para .
Resolvendo as integrais, chegamos que o campo elétrico resultante no ponto é:
Passo 2
b) Assumindo que o potencial elétrico é nulo num ponto infinitamente distante de , podemos escrever a seguinte expressão
já que a distância é constante. Resolvendo essa integral, obtemos que o potencial produzido no ponto é: