P2 de Física 3 da USP - 2019

A figura abaixo mostra trechos de um fio condutor reto e uma fita condutora de comprimentos e , respectivamente. A fita possui largura e sua espessura pode ser desconsiderada. Correntes e percorrem o fio e a fita, respectivamente. A densidade linear de corrente na fita é uniforme .

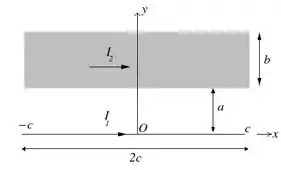
1. Usando a Lei de Biot-Savart, calcule o vetor campo magnético produzido pelo fio num ponto situado ao longo do eixo .
2. Considerando que agora o fio é infinito, , e a fita é infinita ao longo da direção , calcule o vetor força por unidade de comprimento produzida pelo fio sobre a fita.

Um fio condutor muito longo e de seção cilíndrica de raio está envolto por uma casca

cilíndrica de raio , formando um cabo coaxial. No fio há uma densidade de corrente

uniforme e na casca uma densidade de corrente superficial , sendo

e constantes positivas. Expresse suas respostas em termos dos parâmetros

dados:

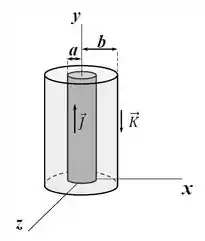
1. Calcule o campo magnético nos pontos onde ( é a distância do ponto até o eixo ).
2. Calcule o campo magnético na região exterior da casca cilíndrica ().
3. Determine o valor de tal que o campo seja nulo na região .

Uma esfera condutora de raio está no interior de uma casca esférica fina condutora de raio . A esfera e a casca esférica são concêntricas e o espaço entre elas está preenchido com

um material de condutividade constante, ( é uma constante positiva). Uma

corrente elétrica , uniformemente distribuída através do material entre os condutores, flui da esfera interna para a casca esférica.

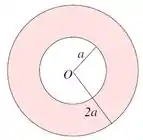
1. Determine a dimensão da constante no Sistema Internacional de Unidades.
2. Calcule a resistência elétrica entre os condutores.
3. Dada uma diferença de potencial aplicada entre as duas superfícies, calcule o vetor densidade de corrente em função dos dados do problema.

Uma corrente estacionária circula no sentido anti-horário de uma espira condutora quadrada, de lado . A figura ao lado mostra a espira em um sistema de coordenadas tal que o plano da espira coincide com o plano . Considere o campo magnético (no mesmo sistema de coordenadas)

1. Calcule as forças magnéticas que atuam em cada um dos lados da espira (como indicados na figura). Calcule também a força resultante sobre a espira.
2. Suponha que o movimento da espira seja restrito a rotações em torno de um eixo vertical fixo passando pelos pontos (veja a figura). Calcule o torque em torno deste eixo em relação à origem.

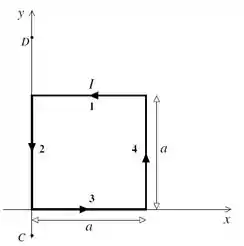
Sugestão para os itens e Calcule primeiramente as forças infinitesimais e em seguida obtenha , efetuando a integral correspondente.