PREC de Física 3 da USP - 2017

A superfície matemática fechada no formato de um cubo de lado mostrada na figura está numa região do espaço onde existe um campo elétrico . Use as equações de Maxwell apropriadas para resolver os itens abaixo.

(a) (1,0 ponto) Calcule o fluxo do campo elétrico através das faces do cubo. Quanta carga existe dentro do cubo?

(b) (0,5 ponto) Calcule a densidade de carga dentro do cubo.

(c) (1,0 ponto) Na região em que se encontra o cubo pode existir um campo magnético , onde é uma constante? Justifique.

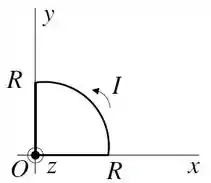
(I) (1,0 ponto) Uma espira plana, contida no plano , é constituída de um segmento circular de raio e dois segmentos retos de comprimento , conforme a figura. Pela espira flui o sentido anti-horário uma corrente . Calcule o vetor campo magnético produzido pela espira no ponto (origem do sistema de coordenadas).

(II) A figura abaixo mostra a seção reta de uma casca cilíndrica muito longa de raio interno e raio externo , coaxial com o eixo . Pela casca flui, na direção positiva do eixo (direção saindo do papel), uma corrente uniformemente distribuída através de sua seção reta.

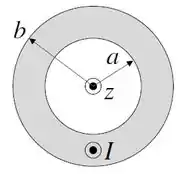
(a) (0,5 ponto) Calcule o vetor densidade de corrente na região , onde é a distância ao eixo da casca cilíndrica.

(b) (1,0 ponto) Calcule o vetor campo magnético na região .

(II) A figura abaixo mostra a seção reta de uma casca cilíndrica muito longa de raio interno e raio externo , coaxial com o eixo . Pela casca flui, na direção positiva do eixo (direção saindo do papel), uma corrente uniformemente distribuída através de sua seção reta.

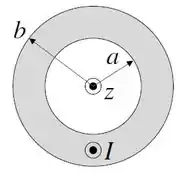
(a) (0,5 ponto) Calcule o vetor densidade de corrente na região , onde é a distância ao eixo da casca cilíndrica.

(b) (1,0 ponto) Calcule o vetor campo magnético na região .

Um solenoide muito longo, coaxial com o eixo , tem comprimento , raio e espiras no total. O solenoide é colocado no vácuo. Desprezando efeitos de borda, o campo dentro do solenoide é , onde é a corrente através das espiras.

(a) (1,0 ponto) Calcula a indutância do solenoide.

(b) (1,5 ponto) Uma corrente variável no tempo dada por percorre o solenoide. Usando a lei de Faraday, calcule o vetor campo elétrico na região , onde é a distância ao eixo do solenoide.

Um solenoide muito longo, coaxial com o eixo , tem comprimento , raio e espiras no total. O solenoide é colocado no vácuo. Desprezando efeitos de borda, o campo dentro do solenoide é , onde é a corrente através das espiras.

(a) (1,0 ponto) Calcula a indutância do solenoide.

(b) (1,5 ponto) Uma corrente variável no tempo dada por percorre o solenoide. Usando a lei de Faraday, calcule o vetor campo elétrico na região , onde é a distância ao eixo do solenoide.

O campo elétrico de uma onda eletromagnética plana monocromática que se propaga no vácuo é dado por , onde e são constantes.

(a) (0,5 ponto) Determine a direção e o sentido de propagação da onda. Calcule o comprimento de onda e a frequência desta onda em função das constantes e .

(b) (0,5 ponto) Que relação deve haver entre e para que o campo satisfaça a equação de ondas eletromagnéticas no vácuo?

(c) (0,5 ponto) Expresse o campo magnético em função de , , e da velocidade da luz no vácuo .

(d) (1,0 ponto) Calcule o vetor de Poynting instantâneo e a densidade de energia média desta onda.

O campo elétrico de uma onda eletromagnética plana monocromática que se propaga no vácuo é dado por , onde e são constantes.

(a) (0,5 ponto) Determine a direção e o sentido de propagação da onda. Calcule o comprimento de onda e a frequência desta onda em função das constantes e .

(b) (0,5 ponto) Que relação deve haver entre e para que o campo satisfaça a equação de ondas eletromagnéticas no vácuo?

(c) (0,5 ponto) Expresse o campo magnético em função de , , e da velocidade da luz no vácuo .

(d) (1,0 ponto) Calcule o vetor de Poynting instantâneo e a densidade de energia média desta onda.