P3 de Física 4 da USP - 2017

Uma partícula de massa m que se move em uma dimensão possui energia potencial que

varia com a posição como mostra a figura.

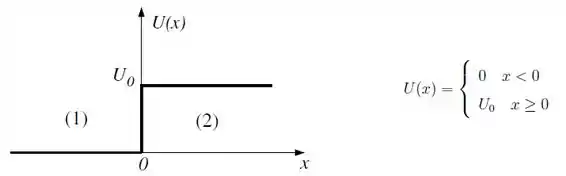
A partícula está em um estado estacionário com energia E φ 1 x   e

da equação de Schrödinger correspondente aos intervalos x ≥ 0

(região 2) respectivamente, são

onde A, B, C e D são constantes arbitrárias.

(a) Determine D. justifique.

(b) Calcule e em função de m, E, U0 e ћ.

(c) Para A = 1, determine B e C.

Uma partícula quântica de massa m executa oscilações harmônicas, em uma dimensão,

num potencial , onde k é a constante da “mola”. Sua função de onda num

estado estacionário é , onde A e b são constantes.

(a) Determine o valor de b (como função de m, k e ћ).

(b) Determine o valor da energia desta partícula neste estado.

(c) Determine o valor médio esperado de neste estado. Deixe sua resposta em função da constante b.

(ii) Um elétron de um átomo de hidrogênio tem os seguintes números quânticos: n = 2, l= 1, = -1 e ms= ½ .

(a) Quanto vale a energia deste elétron?

(b) Quanto vale a componente do momento angular orbital deste elétron na direção do eixo z?

Um elétron está confinado dentro de uma caixa quadrada de lado a, mostrada na figura abaixo.

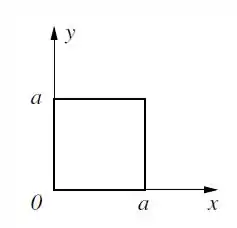
Os estados estacionários normalizados deste elétron são dados por

Onde n,m são números inteiros positivos. A energia de cada um destes estados é dada por

Onde é a massa do elétron

1. Determine a probabilidade de encontrar o elétron na região do plano , para m e n quaisquer.
2. Quais são os 4 pares de valores distintos dos números quânticos n e m correspondentes às três menores energias?
3. Quantos elétron são necessários para preencher completamente os estados com as energias calculadas no item (b)? Suponha que os elétrons não interagem entre si e leve em conta principio de exclusão de Pauli.

(i) Estime o valor da incerteza mínima na velocidade de um elétron não relativístico que está confinado em um poço de potencial unidimensional de largura igual a m. Dado: massa do elétron .