P1 de Física B - FIS1026 da PUCRIO - 2014.1

O GPS de um avião indica que ele está apontado para leste e seu indicador de velocidade em relação ao ar marca . Contudo, um forte vento constante cuja velocidade é de em relação ao solo passa a soprar para o norte. Se o piloto deseja continuar a voar para leste, como indica o GPS, para que direção ele deve apontar o avião?

a) em direção nordeste

b) em direção sudoeste

c) em direção noroeste

d) em direção sudeste

Uma partícula cuja massa é está sujeita à duas forças e simultaneamente, onde e estão em . Encontre o módulo da aceleração resultante e o ângulo que ela faz com o eixo positivo.

a) e

b) e

c) e

d) e

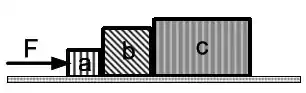
Uma força igual a (N) atua sobre o bloco , como mostrado na figura abaixo, fazendo com que os blocos , e se desloquem sobre uma superfície horizontal sem atrito. Considere que as massas dos blocos são , e , respectivamente. Encontre o vetor força que o bloco exerce sobre o bloco .

a)

b)

c)

d)

Em uma competição de uma olimpíada de inverno um esquiador de massa deve descer uma pista de neve em formato de de círculo de raio , como ilustrado ao lado. Sabendo que ele parte do repouso e que a razão entre o quadrado da sua velocidade e a altura é igual ao dobro da aceleração da gravidade , responda os itens abaixo em função de , e . Considere o atrito desprezível.

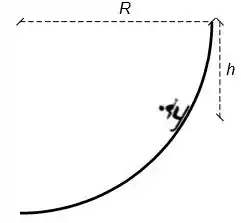
a) Faça um diagrama de corpo livre representando as forças que agem no esquiador, quando ele está à meia altura da pista.

b) Nesta posição, calcule o módulo da velocidade do esquiador e direção que ela faz com eixo vertical.

c) Ainda nesta posição, calcule o módulo da aceleração resultante.

d) Agora o esquiador chega no final da pista. Calcule nesta posição a força normal que a neve faz sobre ele.

Considere as polias e as cordas ideais para o dispositivo da figura abaixo. Despreze suas massas e o atrito das cordas com as polias. Como a polia que sustenta o bloco 2 é móvel, o módulo da aceleração do bloco 1 equivale ao dobro do módulo da aceleração do bloco 2. Adote os valores para as massas dos blocos e . A inclinação do plano é . Não há atrito entre o bloco 1 e o seu plano de apoio. Utilize .

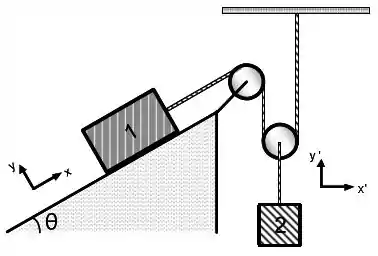
a) Represente o diagrama do corpo livre e escreva as equações de movimento em termos de suas componentes para os dois blocos e a polia móvel presa ao bloco 2. Utilize os sistemas de coordenadas fornecidos para cada componente do sistema.

b) Calcule o vetor aceleração de cada um dos blocos, usando como referência o sistema de coordenadas convencional apresentado para o bloco 2.

c) Considere agora que há atrito entre o bloco 1 e sua superfície de apoio. Reescreva as equações de movimento e determine o coeficiente de atrito mínimo necessário para que o sistema se mantenha em repouso.