Considere as polias e as cordas ideais para o dispositivo da figura abaixo. Despreze suas massas e o atrito das cordas com as polias. Como a polia que sustenta o bloco 2 é móvel, o módulo da aceleração do bloco 1 equivale ao dobro do módulo da aceleração do bloco 2. Adote os valores para as massas dos blocos e . A inclinação do plano é . Não há atrito entre o bloco 1 e o seu plano de apoio. Utilize .
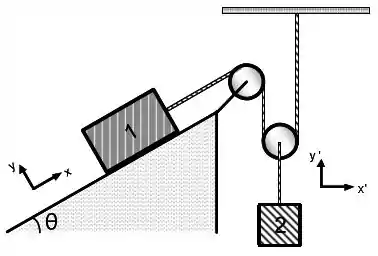
a) Represente o diagrama do corpo livre e escreva as equações de movimento em termos de suas componentes para os dois blocos e a polia móvel presa ao bloco 2. Utilize os sistemas de coordenadas fornecidos para cada componente do sistema.
b) Calcule o vetor aceleração de cada um dos blocos, usando como referência o sistema de coordenadas convencional apresentado para o bloco 2.
c) Considere agora que há atrito entre o bloco 1 e sua superfície de apoio. Reescreva as equações de movimento e determine o coeficiente de atrito mínimo necessário para que o sistema se mantenha em repouso.
Passo 1
a)
Temos o seguinte diagrama:
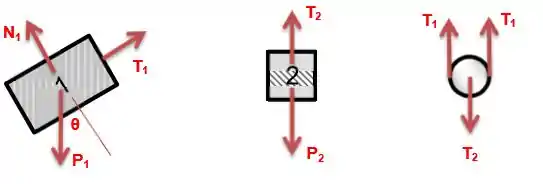
Para o bloco 1:
Eixo :
Eixo :
Para o bloco 2:
Eixo :
Para a polia:
Eixo :
Passo 2
b)
Da equação temos e por causa da roldana móvel: e .
Multiplicando a equação por 2 e substituindo a equação na equação temos:
Somando a equação e a equação temos que:
As acelerações no sistema de coordenadas solicitado são:
Passo 3
c)
Na eminência de movimento:
Para o bloco 1:
Eixo :
Eixo :
Para o bloco 2:
Eixo :
Para a polia:
Eixo :
Resolvendo o sistema para temos:
Resposta
a)
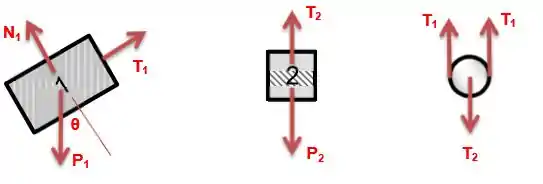
Bloco 1:
Bloco 2:
Polia:
b) ;
c)