Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Conservação da Velocidade e Posição do Centro de Massa

Ver Teoria
Exercício 3012345678910111213141516171819202122232425262728293132333435363738

Enunciado

Uma partícula em repouso está sobre uma mesa horizontal com atrito desprezível e cujo centro de massa coincide com a origem de coordenadas x y . No instante t = 0 ela explode em três partículas menores. A partícula 1 se afasta da origem de coordenadas com um momento linear p 1 → = 12   î   k g m s . A partícula 2 se afasta da origem com um momento linear p 2 → = 6 j ^   k g m s .

a) Determine o momento linear da partícula 3   p 3 → e o ângulo que ele faz em relação ao eixo 𝑥 positivo.

b) Sabendo que a explosão dura 3   m s , calcule as forças responsáveis pela explosão e mostre que durante este processo Σ F → = 0 .

c) Calcule a posição do centro de massa do sistema 1   s após a explosão.

Passo 1

a)

Opaa!! A gente até estranha quando temos uma questão de física sem desenho!! Nada de pânico!! Tudo suave!!

A gente nem precisa de desnho, olha só.

Não teve nenhuma força (externa a partícula) que fez ela explodir, certo? Então foi um processo interno... Quando isso acontece, o momento linear é conservado!!

Passo 2

a)

∆ p → = 0

p 1 → + p 2 → + p 3 → = 0

6 j ^ + 12 î + p 3 → = 0

p 3 → = - 6 j ^ - 12 î   k g   m / s

Show!!!!

Agora, pra descobrir o ângulo, é só desenhar:

O ângulo que a gente quer saber é aquele marcado em vermelho ali, olha a maldade!! A gente quer o ângulo com o eixo x POSITIVO. Não é o ângulo com a parte negativa do eixo x, beleza?

A gente sabe que o vetor p 3 → = - 6 j ^ - 12 î , então o módulo da componente em x é 12, e o módulo da componente em y é 6. Logo, temos:

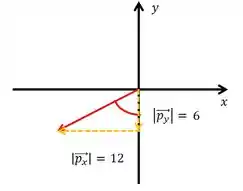
Olha que lindo! Um triângulo retângulo!!!

A gente sabe os catetos, que são os módulos das componentes, então, calculando o arcotangente, para descobrirmos o ângulo:

θ = a r c t g   12 / 6 = 63,4 °

Show. Vamos pra próxima.

Passo 3

b)

O que acontece quando temos uma força? Uma variação do momento da partícula em um intervalo de tempo, certo? A velocidade dela muda.

F 1 → + F 2 → + F 3 → = ∆ p 1 ∆ t + ∆ p 2 ∆ t + ∆ p 3 ∆ t

Substituindo os valores,

∆ p 1 ∆ t + ∆ p 2 ∆ t + ∆ p 3 ∆ t = 12 0,003 î + 6 0,003 j ^ - 12 0,003 î - 6 0,003 j ^ = 0

A soma de todas as forças realmente deu zero!!! Moleza?? Vamos pra próxima

Passo 4

c)

O que a gente acabou de ver na letra b? Que a força resultante é nula, né? Então o momento linear se conserva, logo a velocidade do centro de massa é constante!!!

Equal era a velocidade do centro de massa?

Olha lá no enunciado: “Uma partícula em repouso”.

Opa!!!

Então a velocidade do centro de massa continua sendo zero e, como a parícula estava na origem, vai continuar lá!

Show??

Resposta

a) p 3 → = - 6 j ^ - 12 î   k g   m / s

θ = a r c t g   12 / 6 = 63,4 °

b) Demonstração.

c) Permanece na origem.

Exercícios de Livros Relacionados

Dois blocos de massas 1,0k g e 3,0k g estão ligados por uma mola e repousam em uma superfície sem atrito. Os blocos começam a se mover um em direção ao outro de modo que o bloco de 1,0k g viaja inicia
O coeficiente de restituição ϵ de uma colisão frontal é definido como a razão entre a velocidade relativa depois da colisão e a velocidade relativa antes da colisão. a) Qual é o valor de ϵ para uma co
Uma bola de 1,2k g cai verticalmente em um piso com uma velocidade de 25m / s e ricocheteia com uma velocidade inicial de 10m / s . (a) Qual é o impulso recebido pela bola durante o contato com o piso
Em uma brincadeira comum, mas muito perigosa, alguém puxa uma cadeira quando uma pessoa está prestes a se sentar, fazendo com que a vitima se estatele no chão. Suponha que a vitima tem 70k g , cai de
Em fevereiro de 1955, um paraquedista saltou de um avião, caiu 370m sem conseguir abrir o paraquedas e aterrissou em um campo de neve, sofrendo apenas pequenas escoriações. Suponha que a velocidade do