Um objeto composto por uma haste muito fina de massa e comprimento e um aro fino de raio e massa é livre para girar em torno dos eixos e. A origem do eixo de coordenadas está no centro do aro e no centro da haste. Nos cálculos utilize 3 números significativos.
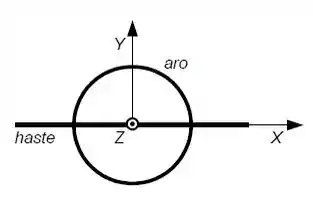
a) Calcule o momento de inércia do objeto em torno dos eixos e . Em torno de qual eixo é mais fácil girar o objeto?
b) O objeto do item anterior é acelerado em torno do eixo . Partindo do repouso, no tempo ele alcança uma velocidade angular . Determine neste instante de tempo quais são os módulos das acelerações tangencial e radial na extremidade da haste.
Passo 1
a)
Fala aí!!! Tudo beleza? Aqui a gente tem um aro com uma haste girando, e três eixos (x, y e z) ele quer saber por qual eixo é mais fácil girar!
Olha que bonito, se eu te perguntasse, ah, tenho um lápis e uma mesa, qual é mais fácil de empurrar? O lápis!!! Porque a massa dele é muito menor do que a da mesa.
Então, como a gente ta falando de rotação o momento de inércia faz o papel da massa nessa história, sacou?
Então é só a gente ver quem tem o menor momento de inércia em relação ao eixo. E então esse vai ser o eixo mais fácil!
Lembrando que temos a haste e os aros. Então temos que calcular o momento de inércia disso tudo em relação a cada eixo! Mas é tranquilão!
Mãos à obra!
Passo 2
Vamos calcular então o momento de inércia do aro em relação aos três eixos, , e .
Os dados da prova são:
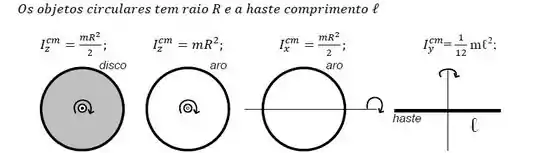
A gente tá falando de disco? Não. Então ignora a primeira.
O segundo é um aro com um eixo passando pelo perpendicularmente pelo centro de massa! OPA!! Isso corresponde ao nosso ! Beleza então:
Agora, na terceira figurinha, temos outro aro com eixo passando pelo diâmetro. OPA! Isso corresponde ao e ao .
Show. Acabou? NÃÃÃO! Isso foi só do aro, tem a haste ainda...
Passo 3
Agora, vamos olhar pro lado direito ali da imagem do passo 2. O momento de inércia da haste que passa pelo CM e gira em torno de um eixo perpendicular a haste é dado... Essa é a situação para os nossos eixos e . Então:
Maravilha...Mas o nosso é diferente, certo? A haste está ao longo do eixo de rotação. Então nesse caso o momento de inércia é zero!!
Passo 4
Vamos achar o momento de inércia conjunto haste e aro para cada eixo, já vou substituir os valores que ele dá pra gente:
E aí, lembra lá da nossa analogia com o lápis e a mesa? Então que é mais fácil de rodar aqui?
O , certo? Porque tem o menor momento de inércia.
Show de bola?
Passo 5
b)
Agora é colocou um movimento ali. Estamos rodando o objeto em torno do eixo
Ele parte do repouso, aí a velocidade inicial é zero.
Ele dá outra informação: .
Nós queremos saber e na extremidade da haste.
Show!! Acompanha comigo
Passo 6
Como a gente tá rodando o objeto, as nossas equações de movimento são as equações da cinemática angular:
Mas ele parte do repouso:
Vamos usar agora a informação que ele deu:
Então:
Beleza!
Mas ele quer e na extremidade da haste
Suaveeeee.. Vem comigo:
A relação entre a aceleração angular (), e linear, que é a tangencial () é:
Onde esse R é o raio do movimento, que nosso caso é metade da barra:
Então:
Show!
Só falta a aceleração na direção radial! Qual que é essa aceleração??
A nossa boa e velha aceleração centrípeta!
Como temos informação a respeito do , e sabemos que:
Lembrando que esse é metade do comprimento da barra, então, substituindo os valores:
Maravilha! Por hoje é tudo pessoal!
Resposta
a)
b)