Um disco de massa e diâmetro e uma corda de massa desprezível e comprimento formam um pêndulo simples, que pode girar sem atrito em torno da origem do sistema de coordenadas ilustrado na figura. O pêndulo é largado do repouso a partir da horizontal. Quando o pêndulo está em sua posição mais baixa, como ilustrado em pontilhado na figura, ele colide com um bloco quadrado de lado e mesma massa, que está em repouso sobre uma superfície horizontal áspera. O coeficiente de atrito cinético entre o bloco e a superfície vale . A colisão ocorre durante o intervalo de tempo de um centésimo de segundo.
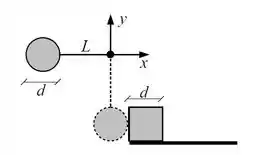
a) Calcule a posição do centro de massa do sistema (disco e bloco) imediatamente antes da colisão.
b) Sabendo que o pêndulo fica parado imediatamente após a colisão, calcule a velocidade do bloco para este instante de tempo.
c)Calcule a força média que o bloco faz no pêndulo durante a colisão.
d) Calcule distância percorrida pelo bloco até parar.
Passo 1
Destaquei algumas informações importantes:
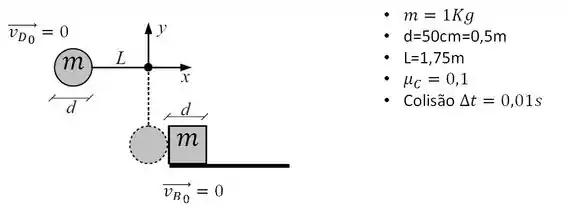
É legal fazer esse tipo de coisa quando estamos resolvendo exercícios. Fazer desenhos e escrever os dados do problema, já colocando tudo em unidade dos SI.
Vamos ler agora o que ele tá querendo que a gente faça na letra a.
Passo 2
a)
Beleza, na letra a ele ta pedindo a posição do centro de massa do sistema bloco mais disco. Show?
Pra isso a gente vai usar:
é o vetor posição do centro de massa do disco.
é o vetor posição do centro de massa do bloco.
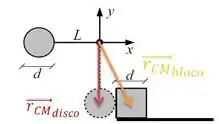
Acompanha comigo aqui:
é o comprimento do fio mais o raio do disco, e aponta pra baixo.
Então:
é o comprimento do fio mais o raio do disco pra baixo mais duas vezes pra direita, certo?
Então:
Substituindo lá na equação para o :
Show. Vamos pra próxima.
Passo 3
b)
Agora, ele quer saber qual é a velocidade do bloco imediatamente após a colisão, sabendo que o pêndulo para.
Vamos separar em dois momentos:
Primeiro, vamos olhar só para o pêndulo. Vamos achar a velocidade dele no ponto mais baixo.
Depois, vamos analisar a colisão de fato.
Acompanha comigo:
Passo 4
Primeiro, estamos falando desta situação:
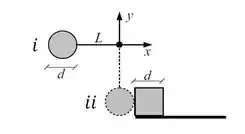
Olhando para o pêndulo nas situações e :
Não temos forças dissipativas, então a energia mecânica se conserva.
No início o pêndulo da parado e o centro de massa dele (centro do disco) está a uma altura 0, em relação ao eixo y.
Na situação , ele tem uma certa velocidade, e o CM está a uma altura em relação a y.
Então a velocidade do disco imediatamente antes da colisão é:
Maravilha! Vamos para o próximo passo e analisar essa colisão.
Passo 5
Durante a colisão, também temos a energia mecânica se conservando.
Vamos chamar de a energia mecânica imediatamente antes da colisão entre o disco e o bloco; e a energia mecânica imediatamente após a colisão:
Antes da colisão, o bloco tá parado, então , já o disco tem velocidade (que calculamos no passo acima), portanto .
Tem variação da energia potencial gravitacional? Não né...Porque durante a colisão não há variação na altura. O enunciada fala pra gente que após a colisão, o disco para, então . E estamos querendo sabe a velocidade do bloco após a colisão, ou seja, nossa incógnita é .
Opa! As massas são iguais. Então a velocidade do bloco é igual a do disco, que a gente calculou no passo anterior:
E aí? Acabou?
É sempre bom dar uma olhada no que a questão tava te pedindo, só pra conferir se fizemos o que ela queria.
E a questão está pedindo . VETOR!
O disco vai andar na horizontal para a direita, então:
Show??Agora tá tudo certo!
Passo 6
c)
A colisão demora um pouquinho, certo? Nesse tempinho o bloco, que tavaparado leva um empurrão do disco e ganha uma velocidade. Até aqui beleza?
Mas se o disco empurra o bloco, então o bloco também empurra o disco. Esse empurrão que o bloco dá no disco é o responsável por fazer a velocidade do disco ir pra zero depois da colisão.
A força média, que é o que ele está pedindo, é a razão entre a variação do momento linear (jáque tem uma variação de velocidade) sobre o tempo da colisão:
Só temos que ficar atentos no enunciado! Olha o que ele tá pedindo: que o bloco faz no pêndulo durante a colisão. Então é a variação de velocidade de quem? Do pêndulo!!!
Ou seja, do disco!
Maravilha, vamos pra próxima.
Passo 7
d)
Então, agora que o bloco tem uma velocidade, ele vai andando na superfície. Mas como essa superfície tem atrito, em algum momento ele vai parar. O atrito é uma força dissipativa que está roubando a energia do bloco.
Vamos ver a que distância isso ocorre, pra isso vamos usar o teorema trabalho x energia cinética.
Lembrando que:
Além disso, o deslocamento e a força de atrito apontam em sentidos opostor, então o ângulo entre eles é . E a
Show?
Resposta
a)
b)
c)
d)