P4 de Física B - FIS1026 da PUCRIO - 2013.2

É permitido o uso de calculador científica simples.

Na figura abaixo, a polia de raio e massa desprezível, gira no sentido horário enrolando um cordão ligado a um bloco. O bloco, por sua vez, está ligado a uma mola ideal que tem sua outra extremidade fixa. A polia gira até que a mola sofra uma deformação de , quando então o sistema entra em repouso. A seguir, a polia é liberada. O atrito no eixo da polia é desprezível, mas há atrito entre o bloco e a superfície de apoio. Despreze a massa do cordão e admita que ele não deslize. Use: massa do bloco ; coeficiente de atrito cinético entre o bloco e a superfície ; constante elástica da mola .

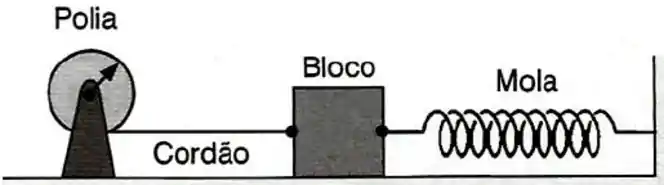
a) Determine a energia mecânica total do sistema quando ele estiver em repouso imediatamente antes da polia ser liberada.

b) Determine a velocidade escalar do bloco quando ele passar pela posição em que a mola está relaxada.

c) Suponha que o bloco andou depois de passar pela posição de relaxamento da mola até entrar em repouso momentaneamente. Determine o deslocamento angular da polia desde que ela foi liberada até este instante.

Considere o sistema de corpos 1 e 2, presos a fios ideais que passam por polias ideais, dado pela figura. Admita como dadas as seguintes grandezas: massas dos dois corpos, coeficientes de atrito cinético () e estático () entre o corpo 2 e plano inclinado, ângulo de inclinação () do plano inclinado em relação à horizontal, aceleração da gravidade local () e o fato do sistema estar inicialmente em repouso.

Obs.: todas as soluções devem partir explicitamente de leis físicas adequadas e possuir desenvolvimento literal.

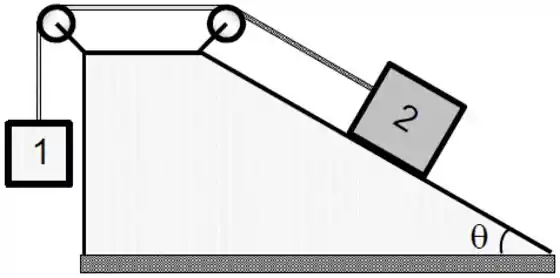
a) O corpo 1 tem massa e o corpo 2 tem massa . O sistema está em equilíbrio estático, na iminência do corpo 2 descer. Faça um diagrama de corpo livre para o corpo 2 nesta situação.

b) Aplique a 2ª Lei de Newton e escreva as equações que relacionam as forças com a aceleração para os dois corpos.

c) Determine a razão entre e para esta situação.

d) Considere agora que o corpo 1 tenha sua massa alterada para , de forma que o corpo 2 sobe o plano inclinado. Faça um diagrama de corpo livre para o corpo 2 nesta situação.

e) Encontre uma expressão literal para o valor da aceleração dos dois corpos.

A lança ilustrada abaixo tem comprimento e massa . Considere a massa uniformemente distribuída. Ela estaria livre para girar, sem atritos, em torno do seu eixo localizado na extremidade inferior (A), contudo, duas forças a mantém em equilíbrio estático fazendo um ângulo com a horizontal. Uma delas tem módulo , está inclinada de em relação à horizontal e atua no centro de massa da lança (B). A outra força tem módulo e atua verticalmente para baixo na extremidade superior da lança (C). Utilize para a aceleração da gravidade.

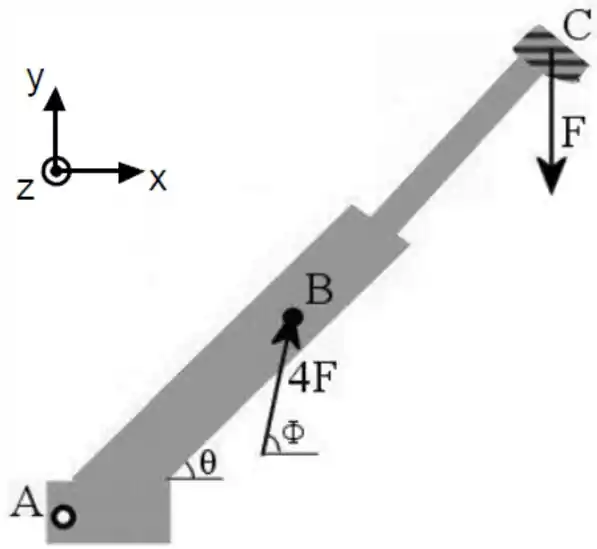
a) Determine os vetores torque em torno de A, produzidos na lança por cada uma das forças e .

b) Suponha agora que as forças e parem de atuar e a lança começa a girar pela ação da força da gravidade. Determine o valor da aceleração angular quando ela passar pela posição horizontal.

c) Continuando seu movimento de rotação, a lança passa pela posição vertical. Determine o valor da velocidade angular nesta posição.