É permitido o uso de calculador científica simples.

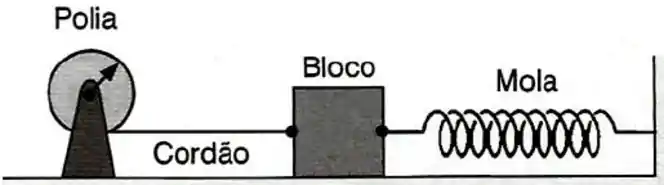
Na figura abaixo, a polia de raio e massa desprezível, gira no sentido horário enrolando um cordão ligado a um bloco. O bloco, por sua vez, está ligado a uma mola ideal que tem sua outra extremidade fixa. A polia gira até que a mola sofra uma deformação de , quando então o sistema entra em repouso. A seguir, a polia é liberada. O atrito no eixo da polia é desprezível, mas há atrito entre o bloco e a superfície de apoio. Despreze a massa do cordão e admita que ele não deslize. Use: massa do bloco ; coeficiente de atrito cinético entre o bloco e a superfície ; constante elástica da mola .

a) Determine a energia mecânica total do sistema quando ele estiver em repouso imediatamente antes da polia ser liberada.

b) Determine a velocidade escalar do bloco quando ele passar pela posição em que a mola está relaxada.

c) Suponha que o bloco andou depois de passar pela posição de relaxamento da mola até entrar em repouso momentaneamente. Determine o deslocamento angular da polia desde que ela foi liberada até este instante.

O sistema está em repouso, então a sua energia cinética é nula!

Vamos considerar a superfície de apoio como o nosso “chão”, ou seja a altura de referência onde a energia potencial gravitacional é nula. A polia, o bloco e a mola estão na altura dessa chão, então a energia potencial gravitacional do nosso sistema é nula!

Só sobrou a energia potencial elástica! E ela é dada por:

sendo a deformação gerada na mola, que foi de . O enunciado também deu .

Ou seja,

Recapitulando,

b)

Depois do instante em que ele está em repouso, o bloco volta pra direita até chegar com uma velocidade na posição em que a mola está relaxada. E a gente quer achar essa !

Pela conservação de energia mecânica, sabemos que quando todas as forças atuando num sistema são conservativas, temos

E quando há forças não-conservativas, a diferença de energia mecânica é igual ao trabalho realizado por essas forças:

Lembrando que as forças não-conservativas são aquelas que fazem o sistema perder energia.

Então vamos dar uma olhada nas forças que atuam no bloco no trajeto dele!

Vejamos, tem as forças:

• peso
• normal
• de tração
• de atrito cinético

A força peso e a força normal a gente sabe que são conservativas. A tração nem sempre é, mas aqui os cordões não deslizam, então supomos que eles são ideais e que, portanto, as forças de tração agindo no bloco não fazem o sistema perder energia.

Só resta a força de atrito , que, justamente, não é conservativa (ou é não-conservativa rs).

Então

Então vamos calcular o trabalho da força de atrito!

A força de atrito é contrária ao sentido do deslocamento, então o trabalho é negativo:

O bloco vai da posição em que a mola está deformada de até onde ela está em relaxada, então a distância é . E o módulo da força de atrito é dado por:

Mas como o bloco não tem nenhum movimento vertical, a normal tem o mesmo módulo que a força peso:

E o enunciado deu , logo:

Então o trabalho é:

Ou seja,

Agora vamos ver o que significa isso:

Sendo o momento inicial, quando o sistema está em repouso, e o momento final, quando o bloco passa pela posição onde a mola está relaxada, isso dá:

Já vimos que no momento inicial a energia cinética e a energia potencial gravitacional são nulas:

E na verdade, o bloco se mantém na mesma altura, deslizando em cima da superfície de apoio, então a energia potencial gravitacional final também é nula:

Outra coisa: no momento final a mola está relaxada, a sua deformação é nula (), então a energia potencial elástica final também vale zero:

Também vimos que a energia potencial elástica da mola quando o sistema está em repouso é:

Opa, isso já adiantou bastante a gente! :)

A equação vai ficar:

Lembrando que a gente chamou a velocidade final do bloco de , isso dá:

Vamos isolar o , depois a gente substitui os valores de e , beleza?

Então temos:

Substituindo e , obtemos:

c)A relação entre deslocamento angular da polia e deslocamento linear do bloco é dada por:

sendo o raio da polia. Os dois são conectados, então tudo que a polia gira o bloco anda, de maneira proporcional ao raio.

O deslocamento linear é o quanto o bloco andou durante o movimento todo. Foram da posição inicial de repouso até a posição onde a mola estava relaxada, mais até parar de novo, logo:

E o raio da polia é , então: