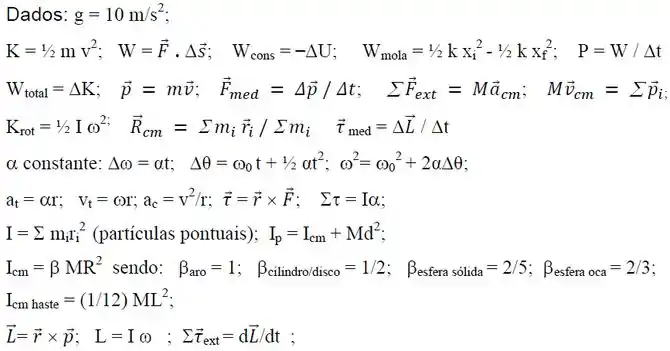
Considere o sistema de corpos 1 e 2, presos a fios ideais que passam por polias ideais, dado pela figura. Admita como dadas as seguintes grandezas: massas dos dois corpos, coeficientes de atrito cinético () e estático () entre o corpo 2 e plano inclinado, ângulo de inclinação () do plano inclinado em relação à horizontal, aceleração da gravidade local () e o fato do sistema estar inicialmente em repouso.
Obs.: todas as soluções devem partir explicitamente de leis físicas adequadas e possuir desenvolvimento literal.
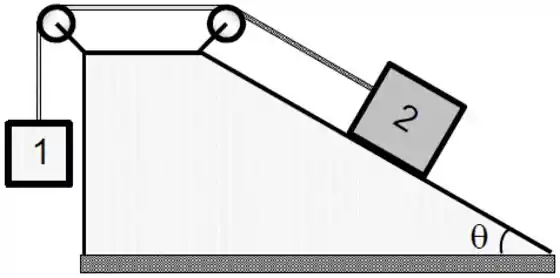
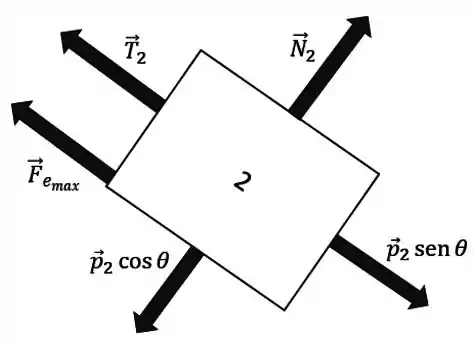
a) O corpo 1 tem massa e o corpo 2 tem massa . O sistema está em equilíbrio estático, na iminência do corpo 2 descer. Faça um diagrama de corpo livre para o corpo 2 nesta situação.
b) Aplique a 2ª Lei de Newton e escreva as equações que relacionam as forças com a aceleração para os dois corpos.
c) Determine a razão entre e para esta situação.
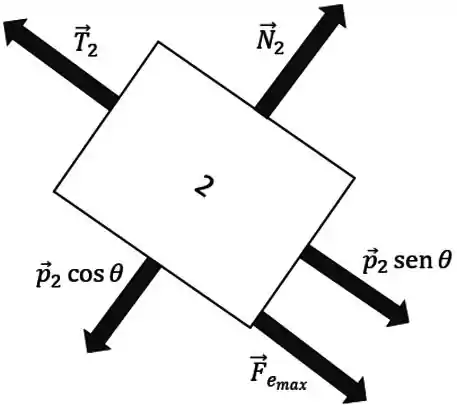
d) Considere agora que o corpo 1 tenha sua massa alterada para , de forma que o corpo 2 sobe o plano inclinado. Faça um diagrama de corpo livre para o corpo 2 nesta situação.
e) Encontre uma expressão literal para o valor da aceleração dos dois corpos.
Passo 1
a)
As forças atuando no corpo 2 são:
- o peso
- a normal
- a tração do fio
- o atrito estático máximo
Passo 2
Então o diagrama de corpo livre do corpo 2 é:
Passo 3
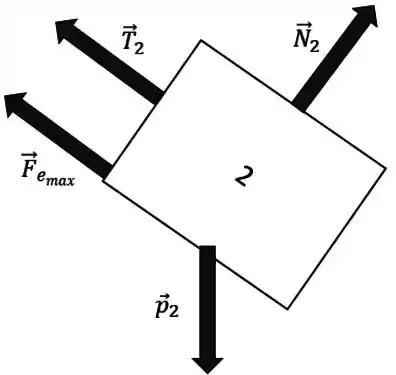
Repare que tanto a normal quanto a tração e a força de atrito são ou paralelas ou perpendiculares ao plano inclinado; só a força peso que não é.
Então uma jogada boa pra gente fazer é definir os eixos coordenados como sendo inclinados, assim ó:
Passo 4
Agora a gente pode usar uma trigonometria básica e decompor a força peso:
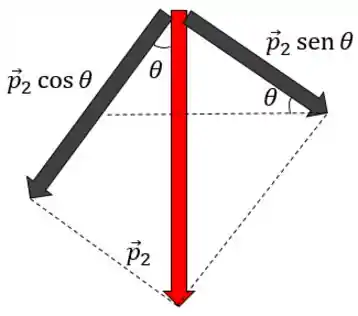
Passo 5
Então o DCL do corpo 2 vai ficar:
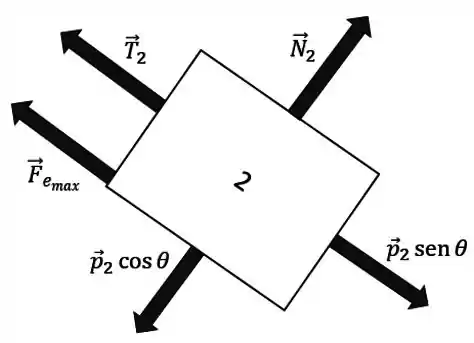
com .
Passo 6
b)
Vamos começar pelo corpo 2, já que a gente fez o diagrama de corpo livre dele.
Pela 2ª lei de Newton, a força resultante atuando nele é:
O corpo está em repouso, então sua aceleração é nula, e consequentemente a força resultante atuando nele também:
E isso vale também separadamente nos eixos e :
Passo 7
No eixo , as forças atuando são a , pra cima, e a , pra baixo:
Passo 8
No eixo , temos a e a , apontando pra esquerda, e a , apontando pra direita. Logo,
E , o módulo da força máxima de atrito estático, é dado por:
Portanto, a equação fica:
Passo 9
Agora vamos pro corpo 1!
O DCL dele é:
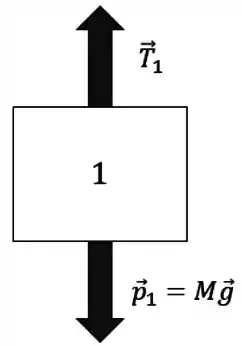
Passo 10
O corpo 1 também está em repouso, então da mesma forma, pela 2ª lei de Newton:
Passo 11
Tem uma coisa importante que a gente não pode deixar escapar: as roldanas e os fios são ideais, então a tração é a mesma nos 2 blocos!
Levando isso em conta, vamos recapitular as equações que achamos até aqui:
Passo 12
c)
Vamos usar esse sisteminha que a gente acabou de achar!
Substituindo a 3ª equação na 1ª, temos:
Dividindo por dos 2 lados:
Passo 13
d)
Antes o corpo 2 estava na iminência de uma descida à direita, então a força de atrito apontava pra esquerda, no sentido contrário à tendência de movimento.
A diferença agora é que o movimento iminente é de subida, pra esquerda. Então a força de atrito estático vai mudar de sentido, e o diagrama de corpo livre é:
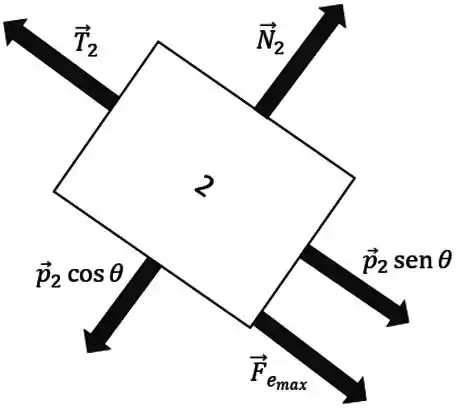
Passo 14
e)
Agora os blocos estão em movimento, e adquirem portanto uma aceleração. Os fios e roldanas são ideais, então não só as trações são iguais, como já vimos, mas as acelerações dos 2 corpos também são iguais, em módulo:
E isso vai ser bem importante!
Passo 15
A força resultante no corpo 1, que está descendo, é:
Aplicando a 2ª lei de Newton:
Logo,
Passo 16
O corpo 2 só se movimenta no eixo , paralelo ao plano, então no eixo a resultante de forças que atuam nele dá zero:
E essas forças são as mesmas de antes: e . Ou seja, novamente temos:
Passo 17
Já no eixo a resultante de forças não é nula, o corpo 2 está subindo, pra esquerda.
Mas atenção, agora que o corpo está em movimento o atrito passa a ser cinético! Então no lugar da entra a , força de atrito cinético.
Ou seja, as forças que atuam no eixo são (pra esquerda), e e (pra direita):
E pela 2ª lei de Newton:
Logo,
Passo 18
E o módulo da força de atrito cinética é dado por:
E já vimos que , logo:
Então, obtemos:
Passo 19
Com isso tudo que achamos, podemos montar um sistema:
Somando as 2 equações, obtemos:
Resposta
a)
b)
c)
d)
e)