Exercícios Resolvidos de Inclinação e deslocamento pelo método dos momentos de área
Ver TeoriaEnunciado
Determine a deflexão em . é constante.
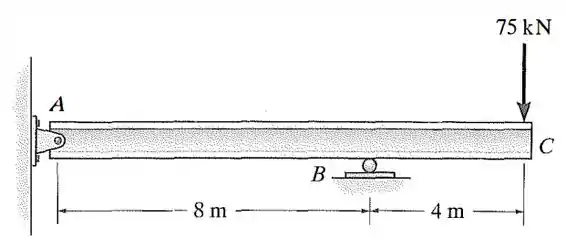
Passo 1
E aí, pessoal!!
Essa questão já um pouquinho mais complexa porque, apesar de pedir as mesmas coisas (inclinação e deflexão) aqui não há engaste. Ou seja, quando a gente for calcular a inclinação utilizando o método da área e vamos ter algo do tipo:
Sendo que agora existe uma inclinação em .
Passo 2
A primeira coisa que temos de fazer é construir o diagrama de momento fletor para a nossa viga. Para isso vamos desenhar as forças de apoio dessa viga:
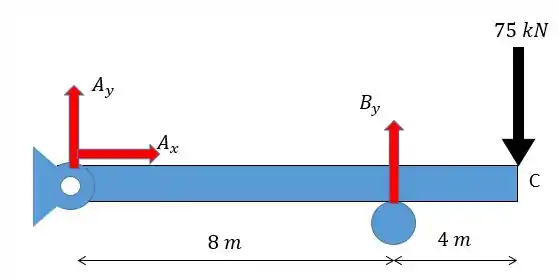
Como só existe uma força em então:
Agora fazendo o somatório das forças em :
Fazendo o somatório dos momentos em relação ao ponto e considerando o sentido anti-horário positivo:
Dessa forma:
Passo 3
Agora vamos colocar essas forças na viga:
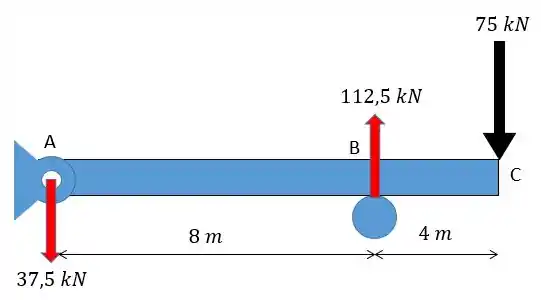
Como só existem forças pontuais o momento fletor cresce e decresce de forma linear tendo o seu máximo no ponto máximo em . Fazendo o corte na seção vamos obter:
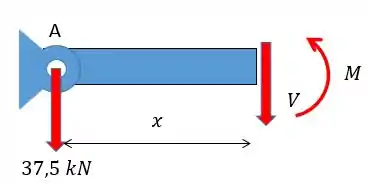
Para achar a força cortante:
Para achar o momento fletor:
Assim, o diagrama ficará da seguinte forma:
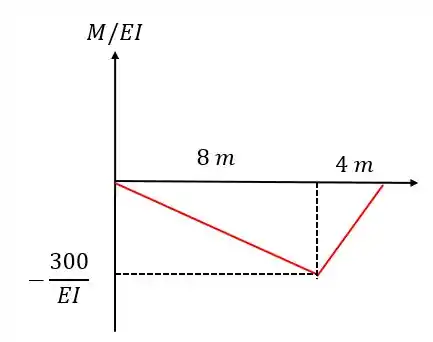
Passo 4
Pessoal, lembram que
Dessa forma a gente precisa saber qual é a inclinação de também.
Gente, vamos resolver esse problema com ajuda na nossa amiga geometria. Que tal fazermos um esboço da linha elástica olha só!
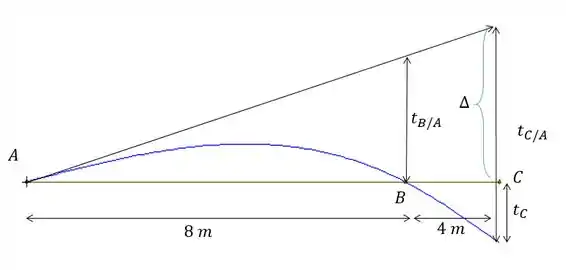
Com isso a gente percebe, pela geometria da figura que:
E esse delta pode ser encontrado por meio de uma semelhança de triângulos (olha para os triângulos de base 8 e 12):
Assim vamos ter:
Dessa forma precisamos achar:
e
Passo 5
Achando :
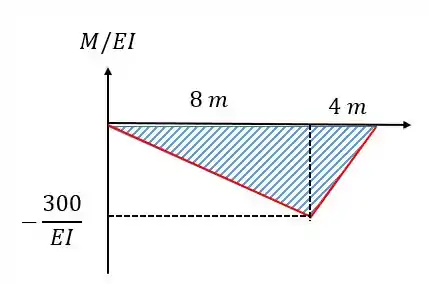
A área é igual a:
O centroide vai estar localizado em:
Mas esse é o valor a partir da origem, nós queremos a partir de , logo:
Assim vamos ter que:
Passo 6
Agora vamos calcular :
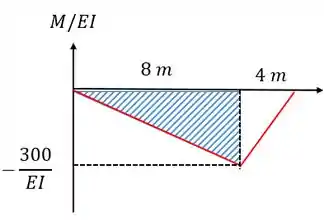
A área é igual a:
O centroide está localizado em:
Assim, vamos ter que:
Passo 7
Agora é só juntar os dois termos: