Exercícios Resolvidos de Inclinação e deslocamento pelo método dos momentos de área
Ver TeoriaEnunciado
Para a viga com carregamento mostrado, determinar a declividade relativa entre e . é constante.
Passo 1
Faaala, galerinha!! Esse problema pede para calcularmos a declividade relativa entre e . Se estamos falando de declividade então estamos falando de ângulo e logo vamos trabalhar com as áreas do diagrama , belezinha? Lembrando que:
Aqui utilizamos e mas podem ser quaisquer dois pontos.
A primeira coisa que vamos fazer netão é montar o diagrama do momento fletor. Depois disso basta calcular a área (tomando alguns cuidados que vou te explicar mais pela frente) e um abraçooo.
Partiu?
Passo 2
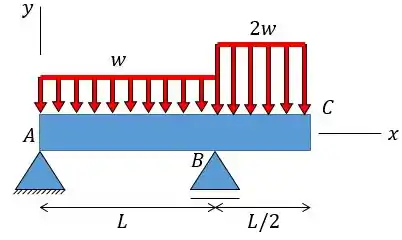
A primeira coisa que temos de fazer é construir o diagrama de momento fletor para a nossa viga. Para isso vamos desenhar as forças de apoio dessa viga assim como as forças concentradas de cada carregamento distribuído:
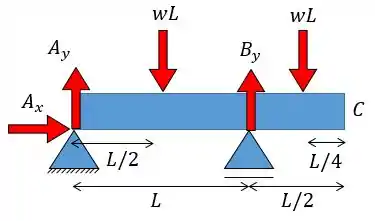
Como só existe uma força em então:
Agora fazendo o somatório das forças em :
E aplicando o somatório dos momentos fletores em vamos ter:
E consequentemente vamos ter:
Passo 3
Agora vamos ver o carregamento na viga:
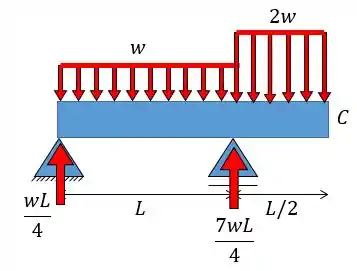
O momento fletor será dado pelas seguintes equações:
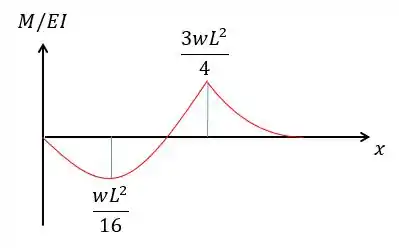
Assim, o diagrama ficará da seguinte forma:
Passo 4
Pessoal, o problema pede a declividade relativa entre e correto? Então faz sentido fazermos:
Basta calcular a área do gráfico entre e :
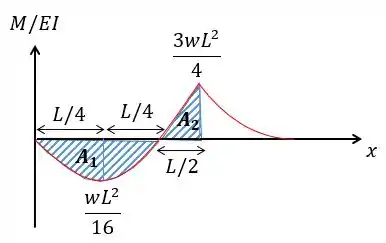
Galerinhaaa, eu sei que o tamanho de ficou menor do que no desenho mas relavaaaa por favor kkkkk foi só um problema técnico...
Galerinha, a gente agora só precisa lembrar que para uma parábola tipo a nós vamos calcular a área conforme a base e a altura:
Logo vamos ter:
Já para a parábola referernte à nós vamos ter que a área é dada também em função de sua base e sua altura mas da forma:
Então no final vamos ter: