Exercícios Resolvidos de Inclinação e deslocamento pelo método dos momentos de área
Ver TeoriaEnunciado
A viga está sujeita à carga mostrada na figura. Determine a inclinação em e o deslocamento em . Considere que o apoio em é um pino e em , um rolete. é constante.
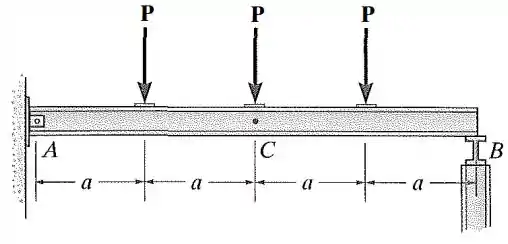
Passo 1
Vamos lá, galera, como essa viga tem um pino e um rolete como apoio, ambos vão ter um deslocamente nulo. Porém, existirá uma inclinação não nula nesses pontos.
O problema pede exatamente a inclinação em (pino) e o deslocamento em . Para isso vamos utilizar o nosso método das áreas.
Primeiro vamos construir o diagrama do momento fletor. Apartir desse diagrama a área será a inclinação e o momento da área o deslocamento. Então partiu?
Passo 2
A primeira coisa que temos de fazer é construir o diagrama de momento fletor para a nossa viga. Para isso vamos desenhar as forças de apoio dessa viga:
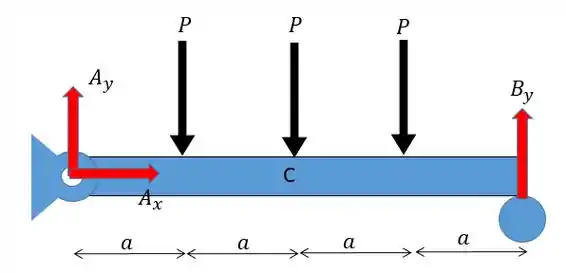
Como só existe uma força em então:
Agora fazendo o somatório das forças em :
Aqui a gente pode lembrar que se trata de um carregamento simétrico então vamos ter que assim:
Passo 3
Agora vamos colocar essas forças na viga:
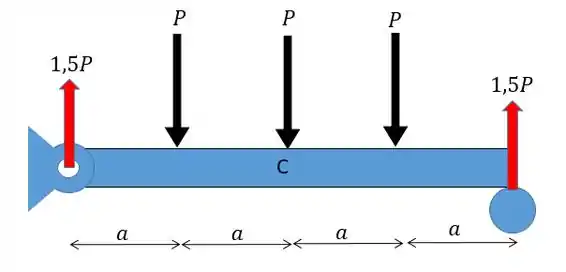
Assim, o diagrama ficará da seguinte forma:
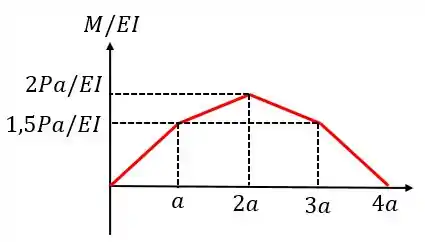
Passo 4
Pessoal, lembram que
Mas como estamos falando de uma viga simétrica então vamos ter que a inclinação no centro é nula.
Logo,
Então basta calcular a área do gráfico entre e :
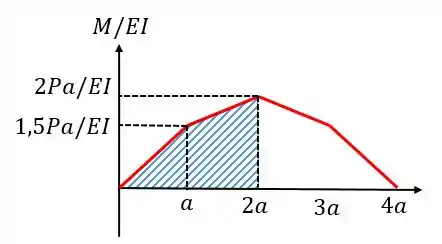
Passo 5
Agora, como o deslocamento em é nulo, para achar o deslocamento em basta fazer:
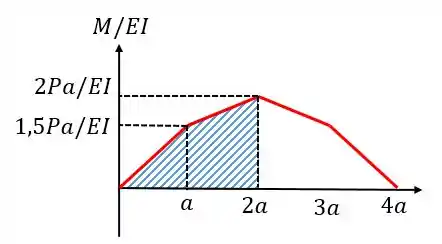
primeiro vamos achar o centroide da figura, para isso vou dividir em um retângulo e dois triângulos:
Simplificando por :
Desta forma vamos ter: