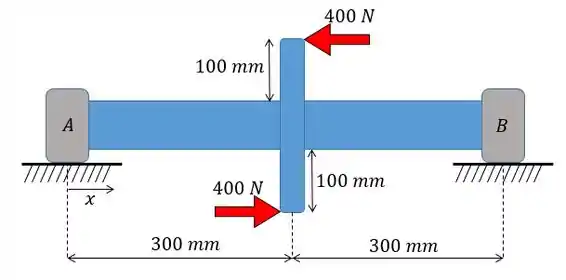
O eixo é suportado por um mancal de apoio em , que exerce somente reações verticais sobre o eixo, e por um mancal de enconsto em , que exerce reações horizontais, bem como reações verticais sobre o eixo. Determine a inclinação do eixo nos mancais. é constante
Passo 1
Fala galera! Temos um probleminha aqui bem legal né, bem prático!? Vamos entender um pouco mais sobre esse problema, temos um eixo submetido a ação de duas forças que juntas causam um momento.

E esse momento aplicado ao eixo, assim como a maioria dos carregamentos irá causar uma deformação. Logo, o estudo da linha elástica faz total sentido aqui e o problema pede o valor da inclinação que esse momento causa. Então vamos utilizar a seguinte relação:
Como podemos ver é necessário utilizar o momento fletor então a primeira coisa que vamos fazer é montar o diagrama . Partiu?
Passo 2
A primeira coisa que temos de fazer então é construir o diagrama de momento fletor para a nossa viga. Para isso vamos desenhar as forças de apoio dessa viga:
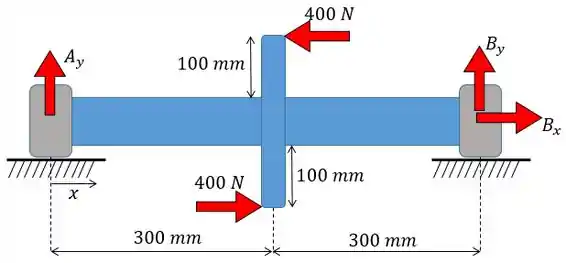
Fazendo o somatório das forças em :
Agora fazendo o somatório das forças em :
Fazendo o somatório dos momentos em relação ao ponto e considerando o sentido anti-horário positivo:
Meus amores aqui vai uma diquinha para vocês, como dito anteriormente a dupla de forças irá realizar um momento, na real essa dupla de forças é considerar um binário e para achar o momento desse binário é só multiplicar a força pela distância entre elas.
Caso você prefira fazer cada força separadamente pode fazer, ok? Esse binário não é nada demais e se não te ajudar você não precisa fazer =D
Voltando ao somatório dos momentos:
Logo,
Passo 3
Agora vamos colocar essas forças na viga:
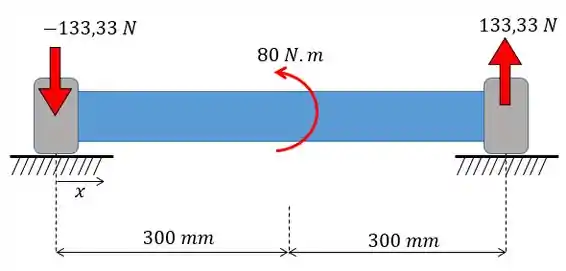
E vamos obter o seguinte diagrama . (Aqui vale lembrar também que esse diagrama é idêntico ao diagrama só do momento fletor já que está dividido por uma constante).
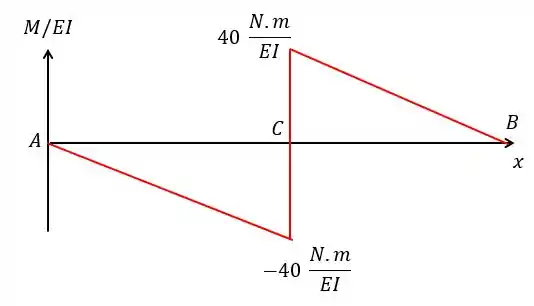
Passo 4
Meus abiguinhos lindos, agora só falta aplicarmos a nossa equaçãozinha!!!
Tá mas e aí quais pontos e eu vou escolher? Que tal pergarmos o ponto médio e a extremidade , assim a nossa equação vai ficar:
Calculando a área entre e e utilizando as medidas em :
Agora vamos fazer entre e e vamos obter:
Somando as duas equações a gente pode achar:
O que faz sentido já que é um problema simétrico, mas não nos fornece nenhum dado muito válido. Logo, vamos analisar o problema a partir das deflexões.
Passo 5
A equação da deflexão é:
Assim vamos achar a deflexão relativa entre e :
Mas essa é a deflexão relativa, a deflexão real entre eles é nula, a gente consegue ver isso com ajuda de um esboço. Aqui repara que vamos utilizar a aproximação , beleza? Podemos fazer isso porque quando falamos de linha elástica temos ângulos bem pequenininhos =D
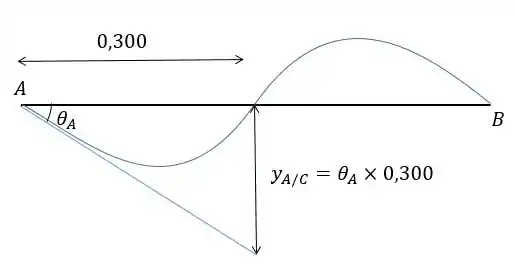
Então a nossa equação é:
Dessa forma vamos ter:
Como ambos os ângulos são iguais então os dois valem: