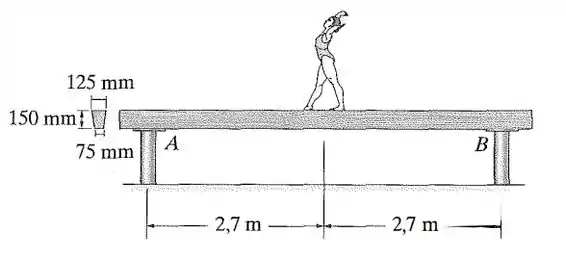
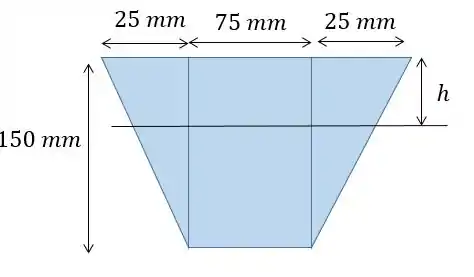
Exercícios Resolvidos de Inclinação e deslocamento pelo método dos momentos de área

Enunciado

Uma ginasta de está em pé no centro da trave (viga) de equilíbrio simplesmente apoiada. Se a trave for feita de madeira e tiver aseção transversal mostrada na figura, determine a deflexão máxima. Consideramos que os apoios em e em são rígidos. .

Passo 1

Galerinha, esse problema é muito parecido com os anteriores e pede a deflexão máxima. A partir daí já podemos saber que essa deflexão máxima ocorre no centro da viga, pelo fato de existir apenas um carregamento central, o peso da ginasta.

Além disso é válido lembrar também que a pesar de não haver inclinação nos apoios, existirá inclinação em ambos. Isso é importante para a resolução.

Vamos começar o problema que nem sempre e fazer um esquema de forças e achar o diagrama do momento fletor.

Partiu!

Passo 2

A primeira coisa que temos de fazer é construir o diagrama de momento fletor para a nossa viga. Para isso vamos desenhar as forças de apoio dessa viga:

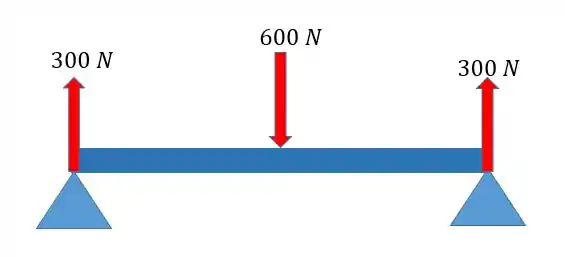
Pessoal, já coloquei direto os valores das reações porque elas tem que ser iguais. Logo se a gente tem uma carga central de então cada reação tem o valor de , ok?

Passo 3

Agora podemos fazer o diagrama de momento fletor, fazendo um corte na barra vamos obter:

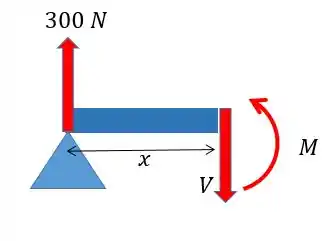
Para achar a força cortante:

Para achar o momento fletor:

O diagrama é simétrico e possui valor máximo em , assim podemos obter:

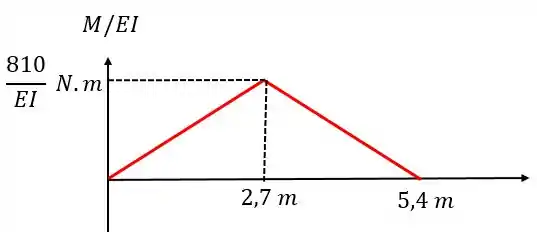
Pessoal, reparem que aqui temos o diagrama do momento fletor sobre , não apenas do momento fletor!

Passo 4

Agora vamos calcular a deflexão máxima, que ocorre no centro. Para isso vamos calcular a área do diagrama que fizemos de modo a achar primeiro a inclinação no ponto médio.

Gente, nessa etapa tentem sempre fazer um esboço da linha elástica, nesse caso vai ficar assim:

Olha só agora como ficou! A tangente em que é nula neste caso, enquanto a tangente em tem uma inclinação. Gente, isso faz sentido dadas as condições de contorno né? (Uma viga simplesmente apoiada vai ter inclinação nas pontas. Como a carga é simétrica o centro não tem inclinação).

De qualquer forma vamos poder calcular o termo da inclinação de com relação à :

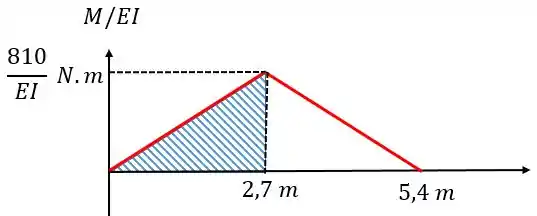
Assim, vamos ter que:

Lembrando que:

Como a inclinação de é nula, vamos ter que:

Passo 5

Agora a gente vai terminar esse problema com um pouquinho de geometria, se liga:

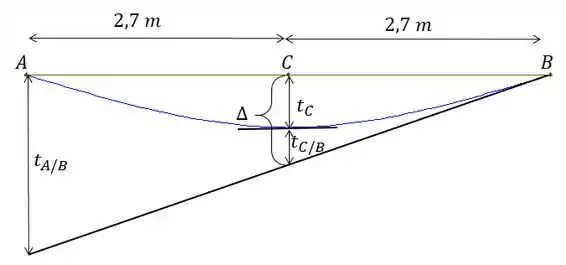
O que queremos achar é a deflexão em , ou seja, . A partir da geometria da figura a gente tem que:

Onde poder ser achado por semelhança de triângulos (um com base de e outro com base de ):

Logo, podemos calcular como:

Agora só precisamos achar e . Para isso vamos voltar ao nosso diagrama. Calculando primeiro vamos ter:

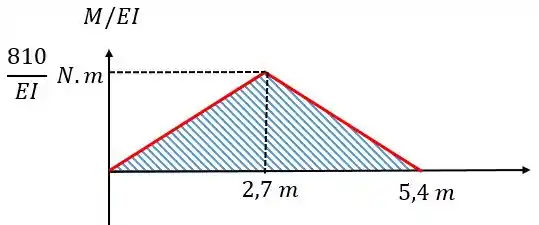
Agora vamos calcular :

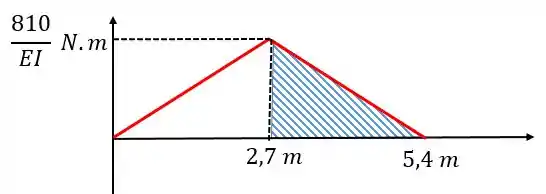
Passo 6

Agora é só juntar os termos:

Assim vamos ter:

Mas ainda falta substituir os termos e .

Passo 7

Calculando o momento de inércia:

Essa equação aí é tabelada ta bom, pessoal?

Agora é só fazer o momento de inércia de cada figura com relação ao eixo que passa pelo centroide, ou seja, a altura h da base maior do trapézio. Dividindo o trapézio em 2 triangulos e 1 retângulo, o momento de inércia dos triângulos é: