Exercícios Resolvidos de Inclinação e deslocamento pelo método dos momentos de área
Ver TeoriaEnunciado
Para a viga com carregamento mostrado, determinar a declividade do ponto . é constante.
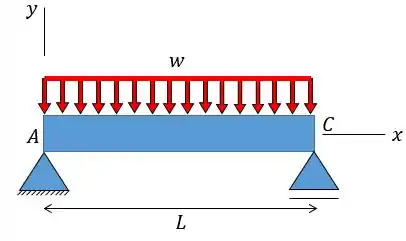
Passo 1
Faaala, galerinha!! Esse problema pede para calcularmos a declividade tanto do ponto quanto do ponto . Se estamos falando de declividade então estamos falando de ângulo e logo vamos trabalhar com as áreas do diagrama , belezinha? Lembrando que:
Aqui utilizamos e mas podem ser quaisquer dois pontos.
A primeira coisa que vamos fazer netão é montar o diagrama do momento fletor. Depois disso basta calcular a área (tomando alguns cuidados que vou te explicar mais pela frente) e um abraçooo.
Partiu?
Passo 2
A primeira coisa que temos de fazer é construir o diagrama de momento fletor para a nossa viga. Para isso vamos desenhar as forças de apoio dessa viga assim como as forças concentradas de cada carregamento distribuído:
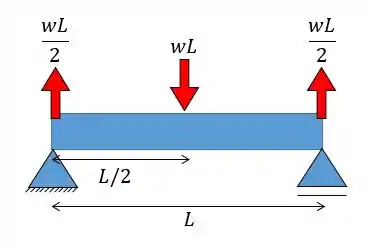
Pessoal, a gente nem precisou fazer muita conta levando em consideração que esse é um problema simétrico não é mesmo? Cada reação é igual à metade do carregamento.
Passo 3
Com o carregamento a gente pode desenhar o diagrama :
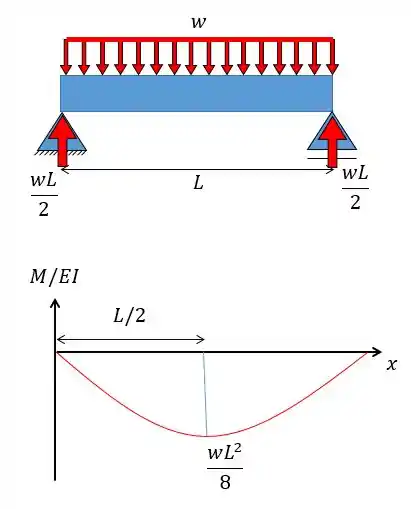
Passo 4
Pessoal, o problema pede a declividade do ponto correto? Então faz sentido fazermos:
Onde é o ponto central da barra. Mas agora vale a observação de que no ponto central a angulação é nula, logo:
Basta calcular a área do gráfico entre e :
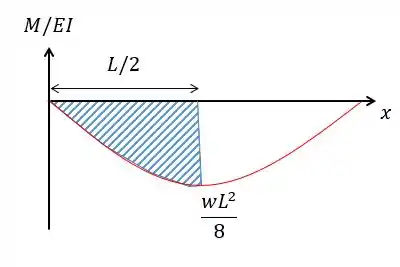
Galerinha, a gente agora só precisa lembrar que para uma parábola nós vamos calcular a área conforme a base e a altura:
Como queremos apenas metade da parábola vamos ter:
Logo vamos ter:
Então no final vamos ter:
Incuímos o sinal negativo porque a área está abaixo do eixo .