Exercícios Resolvidos de Inclinação e deslocamento pelo método dos momentos de área

Enunciado

Determine a inclinação e a deflexão em . é constante.

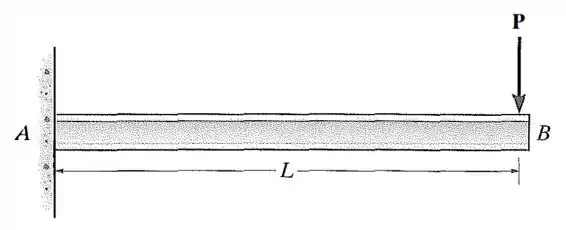
Passo 1

Pessoal, aqui o problema pede para calcular a inclinação que é dada por e a deflexão que é o termo ou , aqui vamos usar . Existem diversas formas de fazer isso mas vamos utilizar a técnica dos momentos de área.

A gente viu dois teoremas que vão nos ajudar o primeiro é para calcular a inclinação. Para isso basta achar a área embaixo do gráfico

Já para achar a deflexão é só pegar o termo que achamos no item acima e multiplicar pelo centroide da área.

Vamos fazer o passo a passo.

Passo 2

A primeira coisa que temos de fazer é construir o diagrama de momento fletor para a nossa viga. Para isso vamos desenhar as forças de apoio dessa viga:

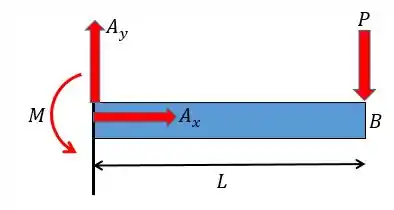
Como só existe uma força em então:

Agora fazendo o somatório das forças em :

Fazendo o somatório dos momentos em relação ao ponto e considerando o sentido anti-horário positivo:

Passo 3

Agora vamos colocar essas forças na viga:

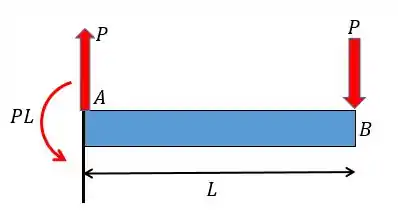
O diagrama ficará da seguinte forma:

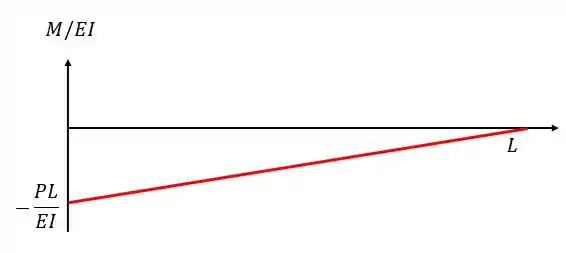
Nesse caso o valor máximo (em módulo) é em , vale e vai se aproximando de zero linearmente até chegar em em

Passo 4

Agora vamos aplicar o primeiro teorema para achar a inclinação em . Para isso é legal construir um esboço de como a deflexão da viga vai ficar:

Para achar esse valor de , que é a inclinação de em relação à inclinação de vamos calcular a área embaixo do gráfico entre e , desta forma vamos ter:

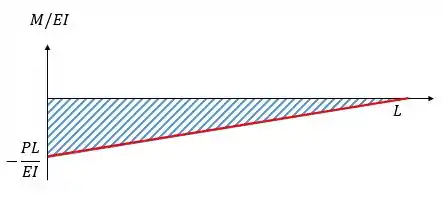
Como não existe inclinação em pelo fato da viga estar engastada então vamos ter:

Assim já temos a inclinação e vale:

Passo 5

Para achar a deflexão basta multiplicar o termo pelo centroide de área que acabamos de utilizar.

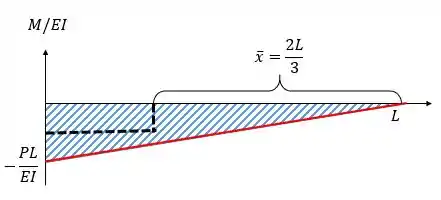
Como o centroide de um triângulo está localizado a uma distância de da extremidade, vamos ter:

obs: Reaparem que precisamos pegar a distância a partir do ponto , pois estamos calculando . Se estivéssemos calculando pegaríamos a distância a partir do ponto .