Exercícios Resolvidos de Inclinação e deslocamento pelo método dos momentos de área
Ver TeoriaEnunciado
Determine a inclinação em e a deflexão em . é constante.
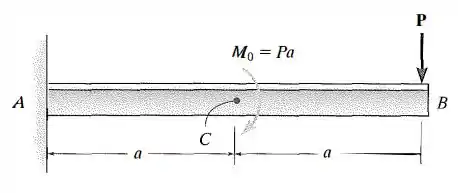
Passo 1
Para achar a inclinação e a deflexão nós vamos utilizar os dois teoremas vistos, lembrando que tanto a inclinação quanto a deflexão são iguais a zero no ponto de engaste.
Antes de mais nada é muito importante que façamos o diagrama do momento fletor e depois vamos calcular a área para achar a inclinação.
Por fim vamos multiplicar a área pelo centroide da área afim de achar a deflexão!
Passo 2
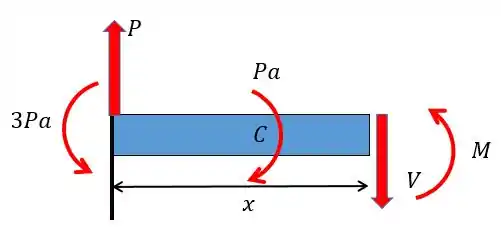
A primeira coisa que temos de fazer então é construir o diagrama de momento fletor para a nossa viga. Para isso vamos desenhar as forças de apoio dessa viga:
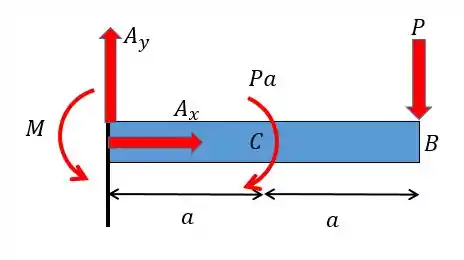
Como só existe uma força em então:
Agora fazendo o somatório das forças em :
Fazendo o somatório dos momentos em relação ao ponto e considerando o sentido anti-horário positivo:
Passo 3
Agora vamos colocar essas forças na viga:
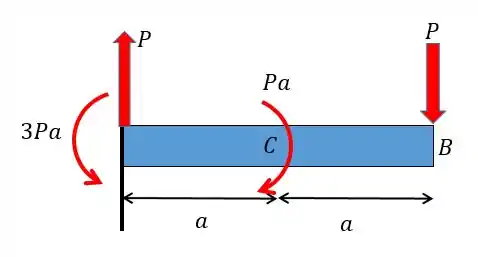
No trecho nós vamos ter que a força cortante vai valer:
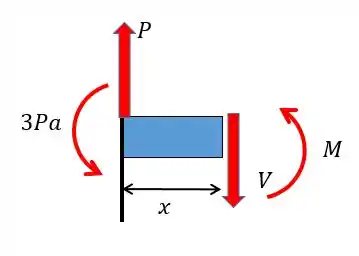
E o momento fletor:
No trecho vamos ter que a força cortante vai valer:
E o momento fletor:
O diagrama ficará da seguinte forma:
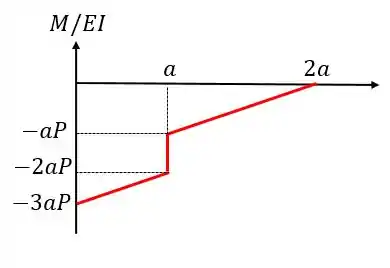
Passo 4
Agora vamos aplicar o primeiro teorema para achar a inclinação em . Para isso é legal construir um esboço de como a deflexão da viga vai ficar:
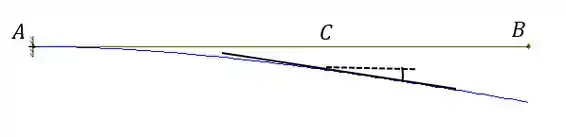
Dando um zoom no ponto vamos obter o seguinte:
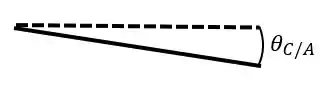
Onde a reta pontilhada é a tangente de (ela tem inclinação zero porque está engastado) e a reta contínua é a tangente de , a gente quer o ângulo entre as duas.
Para achar esse valor de vamos calcular a área embaixo do gráfico entre e , desta forma vamos ter:
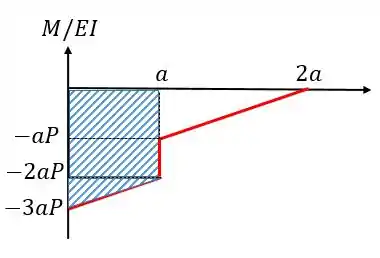
Como não existe inclinação em pelo fato da viga estar engastada então vamos ter:
Assim já temos a inclinação e vale:
Passo 5
Agora vamos calcular a deflexão em para isso a gente tem que achar a inclinação em , ou seja a área do gráfico abaixo.
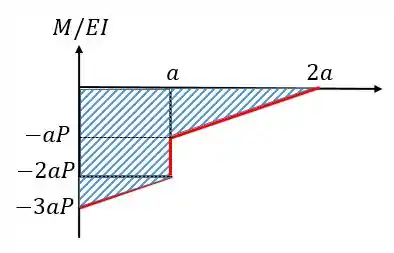
A área vai ser igual a:
Agora, para achar a deflexão precisamos também do centroide da área. Calculando esse centroide vamos ter:
Lembre-se que a posição do centroide tem o o ponto como referência!
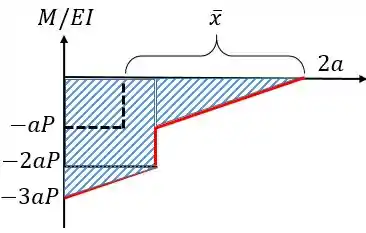
Para facilitar vamos encontrar a posição do centroide de cada uma das três figuras (os dois triângulos e o retângulo) em relação à origem:
Podemos cortar um e o termo :
Mas como queremos em relação à e não em relação à origem vamos ter:
E agora é só multiplicar na área
Vamos obter: