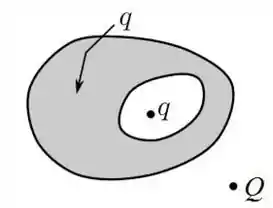
Um condutor com uma cavidade encontra-se em equilíbrio eletrostático e possui uma carga total . No interior da cavidade, existe uma partícula em repouso, de carga também e próximo a este condutor, no seu exterior, foi colocada uma carga .
Qual é o valor da carga total nas superfícies interna e externa deste condutor, respectivamente?
- e
- e
- e
- e
- e
Passo 1
Como o campo elétrico dentro do condutor é nulo, temos que na cavidade interna a distribuição de carga será tal a blindar a carga no interior da cavidade, logo
Passo 2
Em um condutor as cargas se distribuem nas superfícies. Assim a carga total do condutor é dada por
Como sabemos que a carga total é e que a carga na superfície interna é temos
Resposta
(A)
Exercícios de Livros Relacionados
Determine X nas seguintes reações nucleares: (a) 1 H+ 9 B e → X+n ; (b) 12 C + 1 H → X ; (c) 15 N + 1 H →4 H e+X . (Sugestão: consulte o Apêndice F.)
Calcule o número de coulombs de carga positiva que estão presentes em 250c m 3 de água (neutra). (Sugestão: um átomo de hidrogênio contém um próton; um átomo de oxigênio contém oito prótons.)
Se um gato se esfrega repetidamente nas calças de algodão do dono em um dia seco, a transferência de carga do pelo do gato para o tecido de algodão pode deixar o dono com um excesso de carga de - 2,00
A atmosfera da Terra é constantemente bombardeada por raios cósmicos provenientes do espaço sideral, constituídos principalmente por prótons. Se a Terra não possuísse uma atmosfera, cada metro quadrad
Uma corrente de 0,300A que atravesse o peito pode produzir fibrilação no coração de um ser humano, perturbando o ritmo dos batimentos cardíacos com efeitos possivelmente fatais. Sea corrente dura 2,00