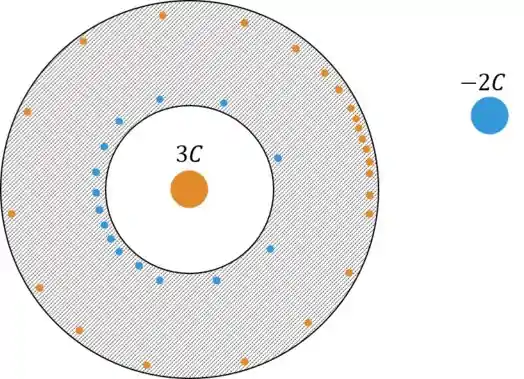
Uma esfera condutora maciça tem um buraco esférico em seu interior, no qual é colocada (utilizando-se magia) uma carga puntiforme de . Ao lado da esfera é colocada uma carga puntiforme de , conforme o desenho:
Dado que a esfera maciça tinha carga total de , calcule a quantidade de cargas em cada uma das superfícies dela (interna e externa) após atingido o equilíbrio eletrostático.
Passo 1
Por indução, na superfície interna vamos ter uma carga de , que é atraída pela puntiforme de no interior da parte oca:
Passo 2
Bom, por conservação de cargas, temos que a carga total no condutor é sempre :
Além disso, ao atingir o equilíbrio eletrostático, só haverá cargas nas superfícies, portanto:
Logo, substituímos os valores:
Note que a carga de no exterior não influi em nada. O único efeito que ela vai ter é de concentrar cargas na parte da superfície que está mais próxima dela, mas o total de cargas lá seria o mesmo, caso esta carga não existisse.