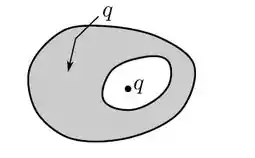
Um condutor com uma cavidade encontra-se em equilíbrio eletrostático e possui uma carga total . No interior da cavidade, existe uma partícula em repouso, de carga também . Quais são as cargas nas superfícies interna e externa do condutor, respectivamente?
(a) e .
(b) e .
(c) e .
(d) e .
(e) e .
Passo 1
Primeiramente vamos analisar a carga no interior da cavidade.
A carga da partícula é . Ela vai atrair cargas de sinal contrário presentes no condutor. Portanto, uma carga total igual a irá se distribuir na superfície interna do condutor.
Podemos ver que a questão já foi resolvida pois a única opção possível agora é a letra (a), mas vamos continuar =)
Passo 2
Como a carga total do condutor é de e nós temos na superfície interna, precisamos compensar essa carga positiva com para que a carga total no condutor seja .
Lembrando que em um condutor as cargas irão se posicionar na superfície externa. A não ser que o condutor possua uma cavidade e que haja uma carga posicionada dentro desta cavidade.
Passo 3
Portanto temos que:
Como eu havia dito, a resposta é a letra (a) =)
Resposta
(a) e .