Encontre o resultado da integral dupla imprópria abaixo:
Onde .
Passo 1
Bem, como em qualquer caso de integral dupla, vamos começar o nosso problema entendendo melhor a região de integração:
- A faixa , significa que a região só pode estar dentro de pedaço
- O problema ainda delimita a faixa pela direita quando ele fala que ...
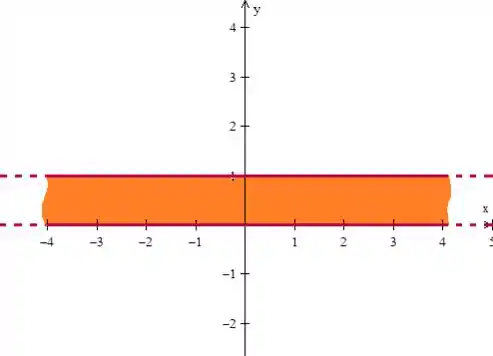
Onde o varia entre e , entende?
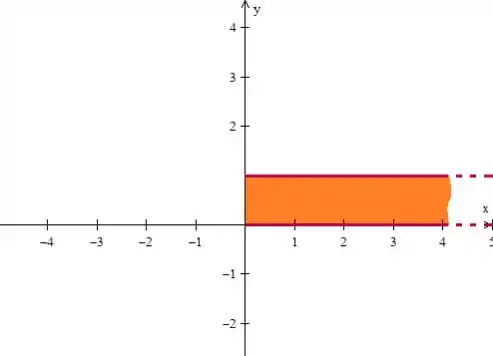
Eis a região 😊!
Passo 2
Você já deve ter notado que a região cresce infinitamente em e esse é o motivo para a integral dupla ser imprópria. Vamos montar aqui essa integral:
Como na região sabemos a variação de e de ...
Basta colocar esses intervalos na integral dupla. MAS ATENÇÃO!!! Na integral mais externa, você deve colocar a variação numérica, que no caso é o intervalo de ...
Veja que como o não tem limite superior, seu limite é o infinito 😉.
Para facilitar os cálculos, tiraremos o infinito da integral e trabalharemos com um limite:
Então agora é só calcularmos a integral dupla mesmo como manda o figurino, ou seja, primeiro a de dentro e depois a de fora. Bora?
Passo 3
Vamos começar com o cálculo da integral de dentro...
Não se assuste com , pois ele é um número qualquer. Pense por exemplo como se ele fosse o número... sei lá, 2. Como a integral é em , é constante...
Para resolvermos essa integral de dentro façamos a mudança de coordenadas...
Derivando em relação a para determinar o ...
Trocando também os limites de integração...
Logo, substituindo tudo na integral...
Substituindo os limites de integração, concluímos que a integral de dentro é...
Passo 4
Pegaremos, em seguida, o resultado anterior e jogar novamente dentro da integral dupla que estamos interessados como faríamos em qualquer integral dupla mesmo...
Como buscamos um limite em (nada a ver com ) podemos tentar tirar o de dentro do limite... Veja bem que...
Então...
Logo, se é constante, o termo pode vazar do limite...
Vamos resolver o limite separado...
Passo 5
Como por propriedade de potência é
Logo...
Passo 6
Por fim, temos que resolver a integral de dentro...
Fazendo uma mudança semelhante a que fizemos anteriormente...
Trocando os limites...
Finalmente, substituindo os limites obtemos...