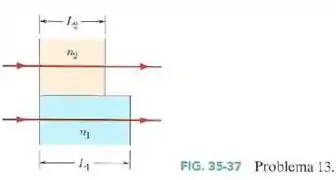
Duas ondas luminosas no ar, de comprimento de onda , estão inicialmente em fase. As ondas passam por camadas de plástico, como na Fig.35-37, com , , e .
- Qual é a diferença de fase, em comprimentos de onda, quando as ondas saem dos dois blocos?
- Se as ondas são superpostas em uma tela, com a mesma amplitude, a interferência é totalmente construtiva, totalmente destrutiva, mais próxima de construtiva ou mais próxima de destrutiva?
Passo 1
a)
Neste caso, a situação do problema mudou um pouco, pois o comprimento de cada meio é diferente. Mas tem uma forma de passarmos por cima disso.
Vamos considerar um meio 3 (o ar) logo depois do meio 2, e considerar a diferença de fase causada pela passagem por 2 em comparação a 1 e depois do meio 3 em comparação ao 1.
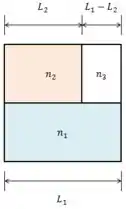
As equações serão, em múltiplos do comprimento de onda:
A diferença de fase total será a soma das duas.
Passo 2
De acordo com o enunciado, temos que , e, como o meio 3 é ar, podemos aproximar seu índice de refração por .
O comprimento de onda da luz incidente é de e a largura de cada meio é e .
A diferença de fase é de 0,833 comprimentos de onda.
Passo 3
b)
A interferência é totalmente destrutiva quando ela é um múltiplo inteiro do comprimento de onda acrescido de meio comprimento de onda (), enquanto ela é totalmente construtiva quando ela é um múltiplo inteiro do comprimento de onda.
Como a diferença de fase está mais próximo de 1 comprimento de onda que de 0,5 comprimentos de onda, a interferência é mais próxima de construtiva.
Resposta
a)
A diferença de fase é de comprimentos de onda.
b)
A interferência está mais próxima de ser construtiva.