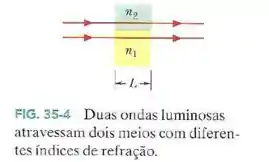
Na Fig. 35-4, suponha que as duas ondas luminosas, cujo comprimento de onda no ar é , têm inicialmente uma diferença de fase de . Os índices de refração dos materiais são e . Determine:
- O menor valor de para o qual as duas ondas estão exatamente em fase depois de atravessar os dois materiais.
- O segundo menor valor de para o qual as duas ondas estão exatamente em fase depois de atravessar os dois materiais.
Passo 1
a)
As ondas inicialmente têm uma diferença de fase .
Além disso, após atravessarem os dois materiais teremos mais uma diferença, devido à diferença de índice de refração dos materiais:
Logo, a diferença de fase total será:
Para eles estarem exatamente em fase, eles devem ter uma diferença de fase de um múltiplo inteiro de . Isso significa que a diferença de fase vai ser de:
Passo 2
O problema nos dá os índices de refração dos materiais, e , e o comprimento de onda da luz incidente no vácuo, .
O menor valor de é aquele dado pela menor diferença de fase possível, que corresponde a . Assim:
Passo 3
b)
Se eu pegar uma diferença de fase e somar , a situação física é a mesma. Como a diferença de fase para interferência construtiva é de , sempre que eu somar a ela eu terei de novo a mesma situação! Por isso que colocamos como condição que .
Com isso, o segundo menor valor de possível corresponde a . Assim:
Resposta
a)
b)