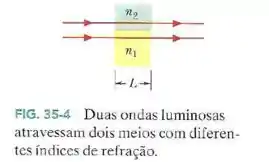
Na Fig. 35-4, suponha que duas ondas com um comprimento de onda de , que se propagam no ar, estão inicialmente em fase.
Uma atravessa uma placa de vidro com um índice de refração e espessura ; a outra atravessa uma placa de plástico com um índice de refração e a mesma espessura.
- Qual é o menor valor de para a qual as ondas deixam as placas com uma diferença de fase de ?
- Se as ondas chegam ao mesmo ponto com a mesma amplitude, a interferência é totalmente construtiva, totalmente destrutiva, mais próxima de construtiva ou mais próxima de destrutiva?
Passo 1
a)
Inicialmente, veja que os dois raios de luz atravessam a mesma distância nos meios com diferentes índices de refração.
Logo, a diferença de fase entre os dois será dada apenas por essa diferença de índice de refração. Como vimos, ela será dada (em radianos) por:
Passo 2
Agora, para usar essa equação, o problema nos dá algumas informações:
Índice de refração do meio 1:
Índice de refração do meio 2:
Comprimento de onda da luz no vácuo:
Diferença de fase na saída:
Assim, substituindo na equação, temos:
Passo 3
Uma observação: por que o problema diz que esse é o “menor valor de ” para essa diferença de fase?
Porque outros valores possíveis seriam , , e por aí vai. Peraí, como assim?!
Acontece que, se somarmos na nossa diferença de fase, nós temos “fisicamente” a mesma situação! Os pontos de uma onda correspondentes ao da outra continuariam sendo os mesmos. Em questões de comprimento, isso equivale a termos mais .
Passo 4
b)
Uma diferença de fase de meio comprimento de onda, que causa interferência totalmente destrutiva, é equivalente a uma diferença de fase de .
Uma diferença de fase de um comprimento de onda, que causa interferência totalmente construtiva, é equivalente a uma diferença de fase de .
Avaliando a nossa diferença de , ela é mais próxima de ser totalmente construtiva.
Resposta
a)
b)
A interferência é mais próxima de totalmente construtiva.